
[番茄花園1] (綜合法)(Ⅰ)證:設(shè)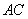 與
與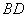 交于點
交于點 ,則
,則 為
為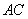 的中點.連
的中點.連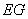 、
、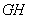 ,
,
又 為
為 的中點,∴
的中點,∴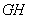
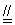
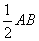 .又
.又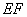
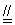
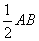 ,∴
,∴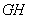
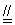
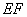 .
.
∴四邊形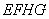 為平行四邊形.
為平行四邊形.
 ∴
∴ .而
.而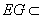 平面
平面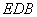 ,∴
,∴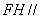 平面
平面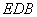 .
.
(Ⅱ)證:由四邊形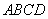 是正方形,有
是正方形,有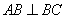 .又
.又 ,
,
∴ .
.
而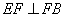 ,∴
,∴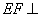 平面
平面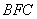 .∴
.∴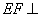
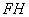 ,
,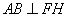 .
.
又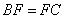 ,
, 為
為 的中點,∴
的中點,∴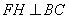 .
.
∴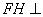 平面
平面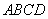 ,∴
,∴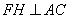 .
.
又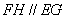 ,∴
,∴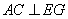 .
.
又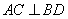 ,
,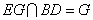 ,∴
,∴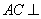 平面
平面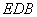 .
.
(Ⅲ)解: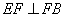 ,
,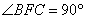 ,∴
,∴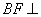 平面
平面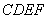 .
.
在平面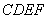 內(nèi)過點
內(nèi)過點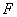 作
作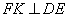 交
交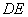 的延長線于
的延長線于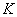 ,則
,則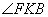 為二面角
為二面角 的一個平面角.
的一個平面角.
設(shè)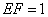 ,則
,則 ,
,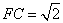 ,
,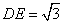 .
.
 又
又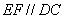 ,∴
,∴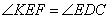 .∴
.∴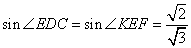 .
.
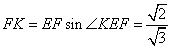 ,
,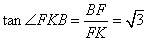 ,∴
,∴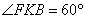 .
.
(向量法):
∵四邊形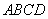 為正方形,∴
為正方形,∴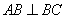 ,又
,又 ,
,
∴ .
.
又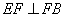 ,∴
,∴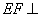 平面
平面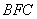 .
.
∴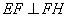 ,∴
,∴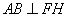 .
.
又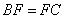 ,
, 為
為 的中點,∴
的中點,∴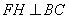 ,∴
,∴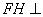 平面
平面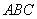 .
.
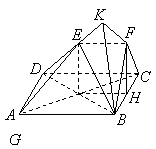
以 為坐標原點,
為坐標原點,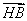 為
為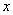 軸正方向,
軸正方向,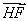 為
為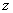 軸正方向,建立如圖所示坐標系.
軸正方向,建立如圖所示坐標系.
設(shè) ,則
,則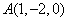 ,
,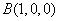 ,
,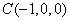 ,
,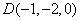 ,
,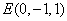 ,
,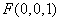 .
.
(Ⅰ)證:設(shè)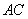 與
與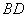 交于點
交于點 ,連
,連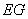 、
、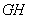 ,則
,則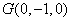 ,
,
∴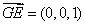 ,又
,又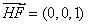 ,∴
,∴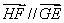 .
.
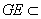 平面
平面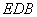 ,
,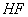 不在平面
不在平面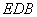 內(nèi),∴
內(nèi),∴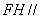 平面
平面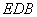 .
.
(Ⅱ)證: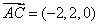 ,
,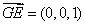 ,
, ,∴
,∴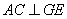 .
.
設(shè)平面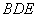 的法向量為
的法向量為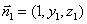 ,
,
則 ,
, ,
,
∴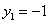 ,
,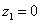 ,即
,即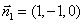 .
.
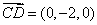 ,
,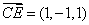 .
.
設(shè)平面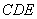 的法向量為
的法向量為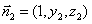 ,
,
則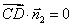 ,
,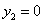 ,
,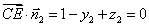 ,
,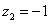 ,故
,故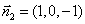 .
.
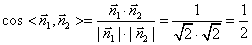 ,
,
∴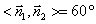 ,即二面角
,即二面角 為
為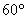 .
.
[番茄花園1]18.


湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com