
【題目】[選修4―4:坐標系與參數方程]
在直角坐標系xOy中,曲線C的參數方程為![]() (θ為參數),直線l的參數方程為
(θ為參數),直線l的參數方程為![]() .
.
(1)若a=1,求C與l的交點坐標;
(2)若C上的點到l的距離的最大值為![]() ,求a.
,求a.
【答案】(1)![]() 與
與![]() 的交點坐標為
的交點坐標為![]() ,
, ![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】試題分析:(1)直線與橢圓的參數方程化為直角坐標方程,聯立解交點坐標;(2)利用橢圓參數方程,設點![]() ,由點到直線距離公式求參數.
,由點到直線距離公式求參數.
試題解析:(1)曲線![]() 的普通方程為
的普通方程為![]() .
.
當![]() 時,直線
時,直線![]() 的普通方程為
的普通方程為![]() .
.
由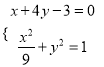 解得
解得![]() 或
或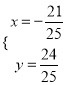 .
.
從而![]() 與
與![]() 的交點坐標為
的交點坐標為![]() ,
, ![]() .
.
(2)直線![]() 的普通方程為
的普通方程為![]() ,故
,故![]() 上的點
上的點![]() 到
到![]() 的距離為
的距離為
![]() .
.
當![]() 時,
時, ![]() 的最大值為
的最大值為![]() .由題設得
.由題設得![]() ,所以
,所以![]() ;
;
當![]() 時,
時, ![]() 的最大值為
的最大值為![]() .由題設得
.由題設得![]() ,所以
,所以![]() .
.
綜上, ![]() 或
或![]() .
.
點睛:本題為選修內容,先把直線與橢圓的參數方程化為直角坐標方程,聯立方程,可得交點坐標,利用橢圓的參數方程,求橢圓上一點到一條直線的距離的最大值,直接利用點到直線的距離公式,表示出橢圓上的點到直線的距離,利用三角有界性確認最值,進而求得參數![]() 的值.
的值.


 寒假創(chuàng)新型自主學習第三學期寒假銜接系列答案
寒假創(chuàng)新型自主學習第三學期寒假銜接系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)= 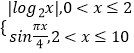 .
.
(1)設函數g(x)=f(x)﹣1,求函數g(x)的零點;
(2)若函數f(x1)=f(x2)=f(x3)=f(x4),且0<x1<x2<x3<x4≤10,求 ![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在四面體ABCD中,E、F分別是AC、BD的中點,若CD=2AB=4,EF⊥AB,則EF與CD所成的角為( )
A.90°
B.45°
C.60°
D.30°
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正三棱錐P﹣ABC底面邊長為6,底邊BC在平面α內,繞BC旋轉該三棱錐,若某個時刻它在平面α上的正投影是等腰直角三角形,則此三棱錐高的取值范圍是( ) 
A.(0, ![]() ]
]
B.(0, ![]() ]∪[
]∪[ ![]() ,3]
,3]
C.(0, ![]() ]
]
D.(0, ![]() ]∪[3,
]∪[3, ![]() ]
]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數y=Asin(ωx+φ)在一個周期內的圖象如圖,此函數的解析式為( ) 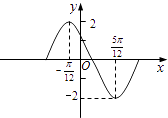
A.y=2sin(2x+ ![]() )
)
B.y=2sin(2x+ ![]() )
)
C.y=2sin( ![]() ﹣
﹣ ![]() )
)
D.y=2sin(2x﹣ ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4—5:不等式選講]
已知函數f(x)=–x2+ax+4,g(x)=│x+1│+│x–1│.
(1)當a=1時,求不等式f(x)≥g(x)的解集;
(2)若不等式f(x)≥g(x)的解集包含[–1,1],求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,平面四邊形ADEF與梯形ABCD所在的平面互相垂直,AD⊥CD,AD⊥ED,AF∥DE,AB∥CD,CD=2AB=2AD=2ED=xAF.
(Ⅰ)若四點F、B、C、E共面,AB=a,求x的值;
(Ⅱ)求證:平面CBE⊥平面EDB;
(Ⅲ)當x=2時,求二面角F﹣EB﹣C的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=2x﹣cosx,{an}是公差為 ![]() 的等差數列,f(a1)+f(a2)+…+f(a5)=5π,則[f(a3)]2﹣a1a5= .
的等差數列,f(a1)+f(a2)+…+f(a5)=5π,則[f(a3)]2﹣a1a5= .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com