試題分析:根據題意,由于函數f(x)=|log
2|x﹣1||,且關于x的方程[f(x)]
2+af(x)+2b=0有6個不同的實數解,解:作出函數f(x)=|log
2|x-1||的圖象,
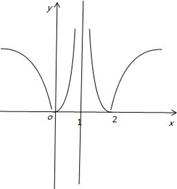
∵方程[f(x)]
2+af(x)+2b=0有6個不同的實數解,∴如圖所示:令t=f(x),方程[f(x)]
2+af(x)+2b=0轉化為:t
2+at+2b=0則方程有一零根和一正根,又∵最小的實數解為-3∴f(-3)=1,∴方程:t
2+at+2b=0的兩根是0和2,由韋達定理得:a=-2,b=0,∴a+b=-2,故選B
點評:解決的關鍵是對于函數與方程的等價轉化思想的運用,屬于基礎題。
