設全集U={1,2,3,4,5,6,7,8,9},若A∩B={2},(∁UA)∩B={4,6,8},(∁UA)∩(∁UB)={1,9},則下列結論中正確的是( )
A.5∈(A∩B)
B.5∉A且5∈B
C.5∈A且5∉B
D.5∉A且5∉B
【答案】
分析:根據題目給出的全集及運算關系A∩B={2},(∁
UA)∩B={4,6,8},(∁
UA)∩(∁
UB)={1,9},分析得到集合A與B的元素情況,從而得到正確的選項.
解答:解:全集U={1,2,3,4,5,6,7,8,9},
因為A∩B={2},說明集合A和集合B中都有2,
由(∁
UA)∩B={4,6,8},說明集合A中沒有4,6,8.集合B中有4,6,8.
又(∁
UA)∩(∁
UB)={1,9},說明集合A中沒有1,9.集合B中沒有1,9.
則集合U、A、B關系如圖,
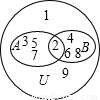
所以集合A中的元素有2,3,5,7.
集合B中的元素有2,4,6,8.
所以,5∈A且5∉B.
故選C.
點評:本題考查了交、并、補集的混合運算,考查了學生對集合運算的理解,考查了綜合分析個判斷問題的能力,是基礎題.



