Question

(1)求橢圓的內接矩形的最大面積;

(2)已知矩形ABCD中,點C坐標為(4,4),A點在曲線x²+y²=9(x＞0,y＞0)上移動,且AB、AD兩邊始終分別平行于x、y坐標軸,求矩形面積ABCD最小時點A的坐標.

Answer 1

解:(1)設內接矩形在第一象限內的頂點為P(acosθ,bsinθ),則有?

S_內接矩形=4S_矩形AOBP=4·acosθ·bsinθ=2absin2θ.?

∵θ∈［0,］,∴2θ∈［0,π］.?

∴S_內接矩形的最大值為2ab.?

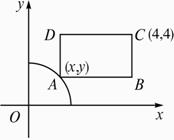
(2)如圖所示,設A(x,y),又設矩形ABCD的面積為S,則有S=(4-x)(4-y)=16-4(x+y)+xy.?

∵A(x,y)在曲線x²+y²=9上,?

∴x²+y²=(x+y)²-2xy=9.?

∴xy=

∴S=16-4(x+y)+

=［(x+y)-4］²+.?

又∵x=3cosθ,y=3sinθ(0＜θ＜),?

∴x+y=3(cosθ+sinθ)=32sin(θ+).?

∵＜θ+＜,∴3＜x+y≤3.?

∴當x+y=4時,S有最小值.?

解方程組

∴A點坐標為()或().