在底面半徑為6的圓柱內,有兩個半徑也為6的球面,兩球的球心距為13,若作一個平面與兩個球都相切,且與圓柱面相交成一橢圓,則橢圓的長軸長為 .
【答案】
分析:設兩個球的球心分別為O
1、O
2,橢圓的長軸為AB,作出由AB與O
1O
2確定平面α與兩個球及圓柱的截面,并過A作O
1O
2的垂線,交圓柱的母線于點C,連接O
1與AB切球O
1的切點D.分別在Rt△O
1DE中和Rt△ABC中,利用∠BAC=∠DO
1E和余弦的定義,結合題中的數據建立關系式,即可解出AB的長,即得該橢圓的長軸長.
解答: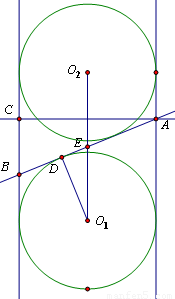
解:設兩個球的球心分別為O
1、O
2,所得橢圓的長軸為AB,
直線AB與O
1O
2交于點E,設它們確定平面α,
作出平面α與兩個球及圓柱的截面,如圖所示
過A作O
1O
2的垂線,交圓柱的母線于點C,設AB切球O
1的大圓于點D,連接O
1D
∵Rt△O
1DE中,O
1E=

O
1O
2=

,O
1D=6
∴cos∠DO
1E=
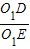
=
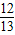
∵銳角∠DO
1E與∠BAC的兩邊對應互相垂直
∴∠BAC=∠DO
1E,
得Rt△ABC中,cos∠BAC=

=

∵AC長等于球O
1的直徑,得AC=12
∴橢圓的長軸AB=13
故答案為:13
點評:本題給出圓柱內兩個與圓柱相切且半徑相等的球,在已知球心距離的情況下求同時與兩個球相切的平面截圓柱得橢圓的長軸的長度.著重考查了圓與圓的位置關系、直角三角形中余弦的定義和橢圓的基本概念等知識,屬于基礎題.

 解:設兩個球的球心分別為O1、O2,所得橢圓的長軸為AB,
解:設兩個球的球心分別為O1、O2,所得橢圓的長軸為AB, O1O2=
O1O2= ,O1D=6
,O1D=6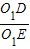 =
=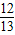
 =
=


 閱讀快車系列答案
閱讀快車系列答案