【題目】根據全球摩天大樓的統計，至2019年，安徽省合肥市的摩天大樓已經有95座在中國城市中排名第10位，全球排名第15位，目前合肥恒大中心建設中的最高樓，外形設計成了“竹節”的形態，既體現了力量超凡，又象征著向上生長的強烈意志，更預示了未來的繁榮和興旺.它與傳承千年的“微文化”相得益建成后將躋身世界十大摩天大樓之列，若大樓由9節“竹節”組成，最上部分的4節高228米，最下部分3節高204米，且每一節高度變化均勻（即每節高度自上而下成等差數列），則該摩天大樓的總高度為（ ）
A.518米B.558米C.588米D.668米
一本好題口算題卡系列答案科目：高中數學 來源： 題型：
【題目】已知曲線
（
為參數），
（
為參數）
（Ⅰ）將
的方程化為普通方程，并說明它們分別表示什么曲線；
（Ⅱ）若
上的點對應的參數為
，
為
上的動點，求
中點
到直線
（為參數）距離的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某芯片公司為制定下一年的研發投入計劃，需了解年研發資金投入量
（單位：億元）對年銷售額
（單位：億元）的影響.該公司對歷史數據進行對比分析，建立了兩個函數模型:①
，②
，其中
均為常數，
為自然對數的底數．
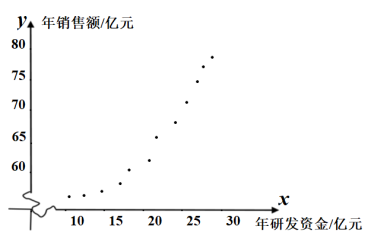
現該公司收集了近12年的年研發資金投入量
和年銷售額
的數據，
，并對這些數據作了初步處理，得到了右側的散點圖及一些統計量的值．令
，經計算得如下數據：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
（1）設
和
的相關系數為
，
和
的相關系數為
，請從相關系數的角度，選擇一個擬合程度更好的模型；
（2）（i）根據（1）的選擇及表中數據，建立關于的回歸方程（系數精確到0.01）；
（ii）若下一年銷售額
需達到90億元，預測下一年的研發資金投入量是多少億元？
附：①相關系數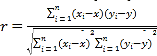
，回歸直線
中斜率和截距的最小二乘估計公式分別為：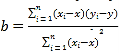
，
；
② 參考數據：
，
，
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】新能源汽車正以迅猛的勢頭發展，越來越多的企業不斷推出純電動產品，某汽車集團要對過去一年推出的四款純電動車型中銷量較低的
車型進行產品更新換代.為了了解這種車型的外觀設計是否需要改進，該集團委托某調查機構對大眾做問卷調查，并從參與調查的人群中抽取了
人進行抽樣分析，得到如下表格：（單位：人）
喜歡 | 不喜歡 | 合計 | |
青年人 |
|
|
|
中年人 |
|
|
|
合計 |
|
|
|
（1）根據表中數據，能否在犯錯誤的概率不超過
的前提下認為大眾對型車外觀設計的喜歡與年齡有關？
（2）現從所抽取的中年人中按是否喜歡型車外觀設計利用分層抽樣的方法抽取
人，再從這人中隨機選出
人贈送五折優惠券，求選出的人中至少有
人喜歡該集團型車外觀設計的概率；
（3）將頻率視為概率，從所有參與調查的人群中隨機抽取
人贈送禮品，記其中喜歡型車外觀設計的人數為
，求的數學期望和方差.
參考公式：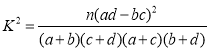
，其中
.
參考數據：
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若函數
對定義域內的每一個值
，在其定義域內都存在唯一的
，使
成立，則該函數為“依附函數”.
(1)判斷函數
是否為“依附函數”，并說明理由；
(2)若函數
在定義域
上“依附函數”，求
的取值范圍；
(3)已知函數
在定義域
上為“依附函數”.若存在實數
，使得對任意的
，不等式
都成立，求實數
的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在極坐標系中，曲線
的極坐標方程為
.現以極點
為原點，極軸為
軸的非負半軸建立平面直角坐標系，直線
的參數方程為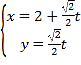
(
為參數).
（1）求曲線的直角坐標系方程和直線的普通方程；
（2）點
在曲線上，且到直線的距離為
，求符合條件的點的直角坐標.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐
中，底面
為梯形，
，
，
，
，面
面，
為
的中點.
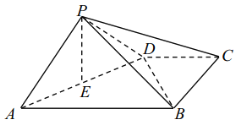
（1）求證：
；
（2）在線段
上是否存在一點
，使得
面
？若存在，請證明你的結論；若不存在，請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
