
求適合下列條件的雙曲線標準方程
(1)虛軸長為12,離心率為![]() .
.
(2)頂點間距離為6,漸近線方程為y=±![]() x.
x.
(3)求與雙曲線x2-2y2=2有公共漸近線,且過點M(2,-2)的雙曲線方程.
|
解:(1)設雙曲線的標準方程為 由題意知2b=12, ∴b=6,c=10,a=8. ∴標準方程為 (2)設以y=± 當λ>0時,a2=4λ, ∴2a=2 當λ<0時,a2=-9λ, ∴2a=2 ∴雙曲線的方程為 (3)設與雙曲線 將點(2,-2)代入得k= ∴雙曲線的標準方程為 解析:(1)由于沒有具體指明雙曲線焦點在哪一個坐標軸上,所以應考慮兩種形式的標準方程;(2)(3)兩小題都是涉及由漸近線求雙曲線方程,應先設出雙曲線的標準方程,再求解. |
|
已知雙曲線的漸近線方程求雙曲線方程時,可利用共漸近線的雙曲線系方程 |


科目:高中數學 來源: 題型:
| x2 |
| 13 |
| y2 |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數學 來源:2012年蘇教版高中數學選修1-1 2.1圓錐曲線練習卷(解析版) 題型:填空題
(8分)求適合下列條件的雙曲線的標準方程:
(1) 焦點在 x軸上,虛軸長為12,離心率為
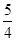 ;
;
(2) 頂點間的距離為6,漸近線方程為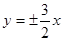 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com