
【題目】在三棱錐![]() ,
, ![]() 和
和![]() 都是邊長為
都是邊長為![]() 的等邊三角形,
的等邊三角形, ![]() ,
, ![]() 、
、![]() 分別是
分別是![]() 、
、![]() 的中點.
的中點.
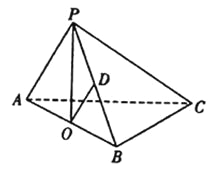
(1)求證: ![]() 平面
平面![]() ;
;
(2)連接![]() ,求證:
,求證: ![]() 平面
平面![]() ;
;
(3)求三棱錐![]() 的體積.
的體積.
【答案】(1)見解析(2)見解析(3)![]() .
.
【解析】試題分析:(1)由三角形中位線定理,得出OD∥PA,結合線面平行的判定定理,可得OD∥平面PAC;
(2)等腰△PAB和等腰△CAB中,證出PO=OC=1,而PC=![]() ,由勾股定理的逆定理,得PO⊥OC,結合PO⊥AB,可得PO⊥平面ABC;
,由勾股定理的逆定理,得PO⊥OC,結合PO⊥AB,可得PO⊥平面ABC;
(3)由(2)易知PO是三棱錐P﹣ABC的高,算出等腰△ABC的面積,再結合錐體體積公式,可得三棱錐![]() 的體積.
的體積.
試題解析:
(1)∵![]() 、
、![]() 分別為
分別為![]() 、
、![]() 的中點.
的中點.
∴![]() .
.
又![]() 平面
平面![]() .
. ![]() 平面
平面![]() .
.
∴![]() 平面
平面![]() .
.
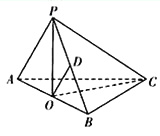
(2)連接![]() .
.
∵![]() ,
, ![]() .
.
∴![]() ,
,
又![]() 為
為![]() 的中點,
的中點,
∴![]() ,
, ![]() ,
,
同理, ![]() ,
, ![]() ,
,
又![]() ,而
,而![]() ,∴
,∴![]() .
.
又![]() .
. ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() .
.
∴![]() 平面
平面![]() .
.
(3)由(II)可知![]() 平面
平面![]() .
.
∴![]() 為三棱錐
為三棱錐![]() 的高,
的高, ![]() .
.
三棱錐![]() 的體積為:
的體積為:
![]() .
.


 英才點津系列答案
英才點津系列答案 紅果子三級測試卷系列答案
紅果子三級測試卷系列答案科目:高中數學 來源: 題型:
【題目】經過函數性質的學習,我們知道:“函數![]() 的圖象關于
的圖象關于![]() 軸成軸對稱圖形”的充要條件是“
軸成軸對稱圖形”的充要條件是“![]() 為偶函數”.
為偶函數”.
(1)若![]() 為偶函數,且當
為偶函數,且當![]() 時,
時,![]() ,求
,求![]() 的解析式,并求不等式
的解析式,并求不等式![]() 的解集;
的解集;
(2)某數學學習小組針對上述結論進行探究,得到一個真命題:“函數![]() 的圖象關于直線
的圖象關于直線![]() 成軸對稱圖形”的充要條件是“
成軸對稱圖形”的充要條件是“![]() 為偶函數”.若函數
為偶函數”.若函數![]() 的圖象關于直線
的圖象關于直線![]() 對稱,且當
對稱,且當![]() 時,
時,![]() .
.
(i)求![]() 的解析式;
的解析式;
(ii)求不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】右圖是一個幾何體的平面展開圖,其中ABCD為
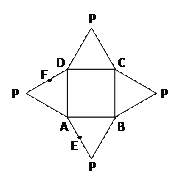
正方形, E、F分別為PA、PD的中點,在此幾何體中,
給出下面四個結論:
①直線BE與直線CF異面;②直線BE與直線AF異面;
③直線EF//平面PBC; ④平面BCE⊥平面PAD.
其中正確結論的個數是
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著霧霾的日益嚴重,中國部分省份已經實施了“煤改氣”的計劃來改善空氣質量指數.2017年支撐我國天然氣市場消費增長的主要資源是國產常規氣和進口天然氣,資源每年的增量不足以支撐天然氣市場連續![]() 億立方米的年增量.進口LNG和進口管道氣受到接收站、管道能力和進口氣價資源的制約.未來,國產常規氣產能釋放的紅利將會逐步減弱,產量增量將維持在
億立方米的年增量.進口LNG和進口管道氣受到接收站、管道能力和進口氣價資源的制約.未來,國產常規氣產能釋放的紅利將會逐步減弱,產量增量將維持在![]() 億方以內.為了測定某市是否符合實施煤改氣計劃的標準,某監測站點于2016年8月某日起連續
億方以內.為了測定某市是否符合實施煤改氣計劃的標準,某監測站點于2016年8月某日起連續![]() 天監測空氣質量指數(AQI),數據統計如下:
天監測空氣質量指數(AQI),數據統計如下:
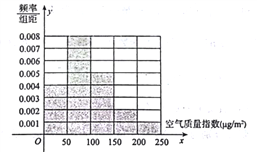
(1)根據上圖完成下列表格
空氣質量指數( |
|
|
|
|
|
天數 |
(2)計算這![]() 天中,該市空氣質量指數的平均數;
天中,該市空氣質量指數的平均數;
(3)若按照分層抽樣的方法,從空氣質量指數在![]() 以及
以及![]() 的等級中抽取
的等級中抽取![]() 天進行調研,再從這
天進行調研,再從這![]() 天中任取
天中任取![]() 天進行空氣顆粒物分析,求恰有
天進行空氣顆粒物分析,求恰有![]() 天空氣質量指數在
天空氣質量指數在![]() 上的概率.
上的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從2名男生和2名女生中任意選擇兩人在星期六、星期日參加某公益活動,每天一人,則星期六安排一名男生、星期日安排一名女生的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)的定義域為D={x|x≠0},且滿足對于任意x1,x2∈D,有f(x1·x2)=f(x1)+f(x2).
(1)求f(1)的值;
(2)判斷f(x)的奇偶性并證明你的結論;
(3)如果f(4)=1,f(x-1)<2,且f(x)在(0,+∞)上是增函數,求x的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com