【題目】已知圓
與圓
關于直線
對稱.
（1）求圓的方程；
（2）過點
作兩條相異直線分別與圓相交于
、
兩點，若直線
、
的傾斜角互補，問直線
與直線
是否垂直？請說明理由.
科目：高中數(shù)學 來源： 題型：
【題目】檳榔原產于馬來西亞，中國主要分布在云南、海南及臺灣等熱帶地區(qū)，在亞洲熱帶地區(qū)廣泛栽培.檳榔是重要的中藥材，在南方一些少數(shù)民族還有將果實作為一種咀嚼嗜好品，但其被世界衛(wèi)生組織國際癌癥研究機構列為致癌物清單Ⅰ類致癌物.云南某民族中學為了解
，
兩個少數(shù)民族班學生咀嚼檳榔的情況，分別從這兩個班中隨機抽取5名同學進行調查，將他們平均每周咀嚼檳榔的顆數(shù)作為樣本繪制成莖葉圖如圖所示（圖中的莖表示十位數(shù)字，葉表示個位數(shù)字）.
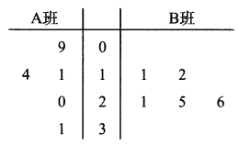
（1）你能否估計哪個班級學生平均每周咀嚼檳榔的顆數(shù)較多？
（2）從班的樣本數(shù)據中隨機抽取一個不超過19的數(shù)據記為
，從班的樣本數(shù)據中隨機抽取一個不超過21的數(shù)據記為
，求
的概率；
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知點
為橢圓
上任意一點，直線
與圓
交于
兩點，點
為橢圓
的左焦點．
（Ⅰ）求橢圓的離心率及左焦點的坐標；
（Ⅱ）求證：直線
與橢圓相切；
（Ⅲ）判斷
是否為定值，并說明理由．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如圖，在多面體
中，平面
平面
，四邊形
為正方形，四邊形為梯形，且
，
，
，
.
（1）求證：
；
（2）若
為線段
的中點，求證：
平面
；
（3）求多面體的體積.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如圖，在正方體
中，點
是底面
的中心，
是線段
的上一點。
（1）若為的中點，求直線
與平面
所成角的正弦值；
（2）能否存在點使得平面
平面
，若能，請指出點的位置關系，并加以證明；若不能，請說明理由。
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】[選修4-4：坐標系與參數(shù)方程]
在直角坐標系
中，曲線
:
（
，
為參數(shù)）.在以坐標原點為極點，
軸的正半軸為極軸的極坐標系中，曲線
：
.
（1）說明是哪一種曲線，并將的方程化為極坐標方程；
（2）若直線
的方程為
，設與的交點為
，
，與的交點為，
，若
的面積為
，求
的值.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】以下四個命題：
①“若
，則
”的逆否命題為真命題
②“
”是“函數(shù)
在區(qū)間
上為增函數(shù)”的充分不必要條件
③若
為假命題，則
，
均為假命題
④對于命題：
，
，則
為：
，
其中真命題的個數(shù)是（ ）
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如果數(shù)列
對于任意
，都有
，其中
為常數(shù)，則稱數(shù)列是“間等差數(shù)列”，為“間公差”.若數(shù)列滿足
，，
.
（1）求證：數(shù)列是“間等差數(shù)列”，并求間公差；
（2）設
為數(shù)列的前n項和，若的最小值為-153，求實數(shù)
的取值范圍；
（3）類似地：非零數(shù)列
對于任意，都有
，其中
為常數(shù)，則稱數(shù)列是“間等比數(shù)列”，為“間公比”.已知數(shù)列
中，滿足
，
，
，試問數(shù)列是否為“間等比數(shù)列”，若是，求最大的整數(shù)
使得對于任意，都有
；若不是，說明理由.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知橢圓
，定義橢圓
上的點
的“伴隨點”為
.
（1）求橢圓
上的點
的“伴隨點”
的軌跡方程；
（2）如果橢圓
上的點
的“伴隨點”為
，對于橢圓
上的任意點
及它的“伴隨點”
，求
的取值范圍；
（3）當
， 
時，直線
交橢圓
于
， 
兩點，若點
， 
的“伴隨點”分別是
， 
，且以
為直徑的圓經過坐標原點
，求
的面積．
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
