
【題目】設f(x)是定義在區間(-∞,+∞)上且以2為周期的函數,對k∈Z,用Ik表示區間(2k-1,2k+1),已知當x∈I0時,f(x)=x2.求f(x)在Ik上的解析式.
【答案】![]()
【解析】試題分析:先根據周期將所求區間Ik轉化到已知區間I0,再代入解析式中即得Ik上的解析式.
試題解析:設x∈(2k-1,2k+1)k∈Z,∴2k-1<x<2k+1,即-1<x-2k<1,
∵x∈I0時,有f(x)=x2,∴由-1<x-2k<1得f(x-2k)=(x-2k)2 ,
∵f(x)是以2為周期的函數,∴f(x-2k)=f(x),
∴f(x)=(x-2k)2,k∈Z.
點睛:函數周期性的判定與應用(1)判定:判斷函數的周期性只需證明f(x+T)=f(x)(T≠0)即可.(2)應用:根據函數的周期性,可以由函數的局部性質得到函數的整體性質,在解決具體問題時,要注意結論:若T是函數的周期,則kT(k∈Z且k≠0)也是函數的周期.


科目:高中數學 來源: 題型:
【題目】(導學號:05856323)已知在△ABC中,A,B,C所對的邊分別為a,b,c,R為△ABC外接圓的半徑,若a=1, ![]() sin2B+
sin2B+![]() sin2C-sin2A=sin Asin Bsin C,則R的值為( )
sin2C-sin2A=sin Asin Bsin C,則R的值為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正方體ABCD-A1B1C1D1的棱長為1,線段B1D1上有兩個動點E,F,且EF=![]() ,則下列結論中錯誤的是( )
,則下列結論中錯誤的是( )
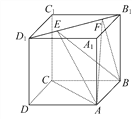
A. AC⊥BE
B. EF∥平面ABCD
C. 三棱錐A-BEF的體積為定值
D. △AEF的面積與△BEF的面積相等
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別是
的左、右焦點分別是![]() ,點
,點![]() 在橢圓
在橢圓![]() 上,
上, ![]() 是等邊三角形.
是等邊三角形.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)點![]() 在橢圓
在橢圓![]() 上,線段
上,線段![]() 與線段
與線段![]() 交于點
交于點![]() ,若
,若![]() 與
與![]() 的面積之比為
的面積之比為![]() ,求點
,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將邊長為![]() 的正方形
的正方形![]() (及其內部)繞
(及其內部)繞![]() 旋轉一周形成圓柱,如圖,
旋轉一周形成圓柱,如圖, ![]() 長為
長為![]() ,
, ![]() 長為
長為![]() ,其中
,其中![]() 與
與![]() 在平面
在平面![]() 的同側.
的同側.
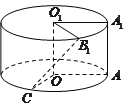
(1)求三棱錐![]() 的體積;
的體積;
(2)求異面直線![]() 與
與![]() 所成的角的大小.
所成的角的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com