Question

已知橢圓

x2

a2

+

y2

b2

=1（a＞b＞0）的左、右焦點分別是F₁（-c，0）、F₂（c，0），Q是橢圓外的動點，滿足|

F1Q

|=2a．點P是線段F₁Q與該橢圓的交點，點T在線段F₂Q上，并且滿足

PT

•

TF2

=0，|

TF2

|≠0．
（Ⅰ）設x為點P的橫坐標，證明|

F1P

|=a+

c

a

x；
（Ⅱ）求點T的軌跡C的方程；
（Ⅲ）試問：在點T的軌跡C上，是否存在點M，使△F₁MF₂的面積S=b²．若存在，求∠F₁MF₂的正切值；若不存在，請說明理由．

Answer 1

<strike id="q00y0"></strike>

分析：（Ⅰ）證法一：設點P的坐標為（x，y）， 由題設條件知| F1P |= (x+c)2+y2 = (x+c)2+b2- b2 a2 x2 = (a+ c a x)2 ， 由此能夠推導出| F1P |=a+ c a x． 證法二：設點P的坐標為（x，y）．記| F1P |=r1，| F2P |=r2， 由r1+r2=2a，r12+r22=4cx，能夠推導出| F1P |=r1=a+ c a x． 證法三：設點P的坐標為（x，y）．橢圓的左準線方程為a+ c a x=0， 由橢圓第二定義得 | F1P | |x+ a2 c | = c a ，由此入手推導出| F1P |=a+ c a x． （Ⅱ）解法一：設點T的坐標為（x，y）．當| PT |=0時，點（a，0）和點（-a，0）在軌跡上． 當| PT |≠0且| TF2 |≠0時，由題設條件知T為線段F2Q的中點． 在△QF1F2中，| OT |= 1 2 | F1Q |=a，由此求出點T的軌跡C的方程． 解法二：在推導出T為線段F2Q的中點的基礎上，設點Q的坐標為（x'，y'）， 由中點坐標公式和| F1Q |=2a推導出點T的軌跡C的方程． （Ⅲ）解法一：C上存在點M（x0，y0）使S=b2的充要條件是 x 2 0 + y 2 0 =a2③ 1 2 •2c|y0|=b2．④ 由③得|y0|≤a，由④得|y0|≤ b2 c ．再分類討論進行求解． 解法二：C上存在點M（x0，y0）使S=b2的充要條件是 x 2 0 + y 2 0 =a2③ 1 2 •2c|y0|=b2．④ 由④得|y0|≤ b2 c ．上式代入③得x02=a2- b4 c2 =（a- b2 c ）（a+ b2 c ）≥0．再分類討論進行求解．

解答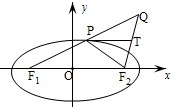：（Ⅰ）證法一：設點P的坐標為（x，y）． 由P（x，y）在橢圓上，得| F1P |= (x+c)2+y2 = (x+c)2+b2- b2 a2 x2 = (a+ c a x)2 由x≥a，知a+ c a x≥-c+a＞0，所以| F1P |=a+ c a x 證法二：設點P的坐標為（x，y）．記| F1P |=r1，| F2P |=r2， 則r1= (x+c)2+y2 ，r2= (x+c)2+y2 ． 由r1+r2=2a，r12+r22=4cx，得| F1P |=r1=a+ c a x． 證法三：設點P的坐標為（x，y）．橢圓的左準線方程為a+ c a x=0 由橢圓第二定義得 | F1P | |x+ a2 c | = c a ，即|| F1P = c a |x+ a2 c |=|a+ c a x|． 由x≥-a，知a+ c a x≥-c+a＞0，所以| F1P |=a+ c a x． （Ⅱ）解法一：設點T的坐標為（x，y）． 當| PT |=0時，點（a，0）和點（-a，0）在軌跡上． 當| PT |≠0且| TF2 |≠0時，由| PT |•| TF2 |=0，得 PT ⊥ TF2 ． 又| PQ |=| PF2 |，所以T為線段F2Q的中點． 在△QF1F2中，| OT |= 1 2 | F1Q |=a，所以有x2+y2=a2． 綜上所述，點T的軌跡C的方程是x2+y2=a2． 解法二：設點T的坐標為（x，y）．當| PT |=0時，點（a，0）和點（-a，0）在軌跡上． 當| PT |≠0且| TF2 |≠0，時，由 PT • TF2 =0，得 PT ⊥ TF2 ． 又，| TF2 || PQ |=| PF2 |，所以T為線段F2Q的中點． 設點Q的坐標為（x'，y'），則 x= x′+c 2 y= y′ 2 . 因此 x′=2x-c y′=2y. ① 由| F1Q |=2a得（x'+c）2+y'2=4a2．② 將①代入②，可得x2+y2=a2． 綜上所述，點T的軌跡C的方程是x2+y2=a2． （Ⅲ）解法一：C上存在點M（x0，y0）使S=b2的充要條件是 x 2 0 + y 2 0 =a2③ 1 2 •2c|y0|=b2．④ 由③得|y0|≤a，由④得|y0|≤ b2 c ．所以，當a≥ b2 c 時，存在點M，使S=b2； 當a＜ b2 c 時，不存在滿足條件的點M． 當a≥ b2 c 時， MF1 =（-c-x0，-y0）， MF2 =（c-x0，-y0）， 由 MF1 • MF2 =x02-c2+y02=a2-c2=b2， MF1 • MF2 =| MF1 |•| MF2 |=cos∠F1MF2， S= 1 2 MF1 • MF2 sin∠F1MF2=b2，得tan∠F1MF2=2． 解法二：C上存在點M（x0，y0）使S=b2的充要條件是 x 2 0 + y 2 0 =a2③ 1 2 •2c|y0|=b2．④ 由④得|y0|≤