
 的圖象可由函數y=sin2x的圖象向左平移
的圖象可由函數y=sin2x的圖象向左平移 個單位得到;
個單位得到;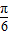 個單位后函數解析式,可以判斷③的真假;
個單位后函數解析式,可以判斷③的真假;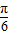 個單位得到函數
個單位得到函數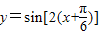 =
=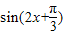 的圖象,故③錯誤
的圖象,故③錯誤

科目:高中數學 來源: 題型:
| A、1個 | B、2個 | C、3個 | D、4個 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| π |
| 6 |
| π |
| 6 |
查看答案和解析>>
科目:高中數學 來源:2011-2012年遼寧省盤錦市高一下學期第二次月考數學試卷(解析版) 題型:選擇題
下列敘述中正確的是( )
A.三角形的內角必是第一象限或第二象限的角
B.角α的終邊在x軸上時,角α的正弦線、正切線分別變成一個點
C.終邊相同的角必相等
D.終邊在第二象限的角是鈍角
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com