
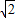 ,0),半徑為1,雙曲線C的兩條漸近線都過原點,且與圓A相切,雙曲線C的一個頂點A′與點A關(guān)于直線y=x對稱.
,0),半徑為1,雙曲線C的兩條漸近線都過原點,且與圓A相切,雙曲線C的一個頂點A′與點A關(guān)于直線y=x對稱.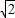 ,試求k的值及此時點B的坐標.
,試求k的值及此時點B的坐標.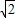 ,設直線l':y=kx+m,則可表示出B點到直線l的距離求得m與k的關(guān)系式,把l'代入雙曲線方程,根據(jù)判別式等于0求得m和k的另一個關(guān)系式,聯(lián)立求得m和k,進而求得B點的坐標.
,設直線l':y=kx+m,則可表示出B點到直線l的距離求得m與k的關(guān)系式,把l'代入雙曲線方程,根據(jù)判別式等于0求得m和k的另一個關(guān)系式,聯(lián)立求得m和k,進而求得B點的坐標.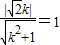 ,解得k=±1.即漸近線為y=±x.
,解得k=±1.即漸近線為y=±x.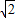 ),
),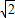 ,雙曲線的方程為
,雙曲線的方程為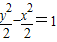 .
.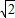 ),(0<k<1).
),(0<k<1).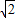 ,設直線l':y=kx+m,則
,設直線l':y=kx+m,則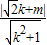 =
=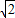 ,即m2+2
,即m2+2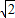 km=2①
km=2①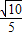 ,k=
,k=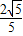 .
.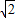 ,y=
,y=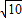 ,所以B(2
,所以B(2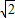 ,
,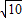 ).
).

科目:高中數(shù)學 來源: 題型:
| 2 |
| 2 |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
| 2 |
| 2 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
(1)求雙曲線C的方程;
(2)設直線l過點A,斜率為k,當0<k<1時,雙曲線C的上支上有且僅有一點B到直線l的距離為![]() ,試求k的值及此時點B的坐標.
,試求k的值及此時點B的坐標.
查看答案和解析>>
科目:高中數(shù)學 來源:2009-2010學年湖北省武漢市外國語學校高二(上)期末數(shù)學試卷(文科)(解析版) 題型:解答題
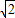 ,0),半徑為1,雙曲線C的兩條漸近線都過原點,且與圓A相切,雙曲線C的一個頂點A′與點A關(guān)于直線y=x對稱.
,0),半徑為1,雙曲線C的兩條漸近線都過原點,且與圓A相切,雙曲線C的一個頂點A′與點A關(guān)于直線y=x對稱.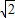 ,試求k的值及此時點B的坐標.
,試求k的值及此時點B的坐標.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com