
【題目】以直角坐標(biāo)系原點O為極點,x軸的正半軸為極軸.已知點P的直角坐標(biāo)為![]() ,點M的極坐標(biāo)為
,點M的極坐標(biāo)為![]() ,若直線l過點P,且傾斜角為
,若直線l過點P,且傾斜角為![]() ,圓C以M點為圓心,4為半徑.
,圓C以M點為圓心,4為半徑.
![]() 求直線l和圓C的極坐標(biāo)方程;
求直線l和圓C的極坐標(biāo)方程;
![]() 直線l與x軸y軸分別交于A,B兩點,Q為圓C上一動點,求
直線l與x軸y軸分別交于A,B兩點,Q為圓C上一動點,求![]() 面積的最小值.
面積的最小值.
【答案】(1)![]() .
.![]() .(2)
.(2)![]() .
.
【解析】
![]() 先求出直線l的直角坐標(biāo)方程,由此能求出直線l的極坐標(biāo)方程,先求出圓C的直角坐標(biāo)方程,由此能求出圓C的極坐標(biāo)方程.
先求出直線l的直角坐標(biāo)方程,由此能求出直線l的極坐標(biāo)方程,先求出圓C的直角坐標(biāo)方程,由此能求出圓C的極坐標(biāo)方程.
![]() 直線l與x軸交與
直線l與x軸交與![]() ,直線l與y軸交于
,直線l與y軸交于![]() ,
,![]() ,圓心到直線l的距離為
,圓心到直線l的距離為![]() ,由此能求出
,由此能求出![]() 面積的最小值.
面積的最小值.
解:![]() 點P的直角坐標(biāo)為
點P的直角坐標(biāo)為![]() ,直線l過點P,且傾斜角為
,直線l過點P,且傾斜角為![]() ,
,
![]() 直線l的直角坐標(biāo)方程為
直線l的直角坐標(biāo)方程為![]() ,即
,即![]() ,
,
![]() 直線l的極坐標(biāo)方程為:
直線l的極坐標(biāo)方程為:![]() .
.
![]() 點M的極坐標(biāo)為
點M的極坐標(biāo)為![]() ,
,![]() 的直角坐標(biāo)為
的直角坐標(biāo)為![]() ,
,
![]() 圓C以M點為圓心,4為半徑,
圓C以M點為圓心,4為半徑,
![]() 圓C的直角坐標(biāo)方程為
圓C的直角坐標(biāo)方程為![]() ,即
,即![]() ,
,
![]() 圓C的極坐標(biāo)方程為:
圓C的極坐標(biāo)方程為:![]() ,即
,即![]() .
.
![]() 直線l與x軸交與
直線l與x軸交與![]() ,直線l與y軸交于
,直線l與y軸交于![]() ,
,![]() ,
,
圓心到直線l的距離為![]() ,
,
![]() 面積的最小值為:
面積的最小值為:
![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】用一個長為![]() ,寬為
,寬為![]() 的矩形鐵皮(如圖1)制作成一個直角圓形彎管(如圖3):先在矩形的中間畫一條曲線,并沿曲線剪開,將所得的兩部分分別卷成體積相等的斜截圓柱狀(如圖2),然后將其中一個適當(dāng)翻轉(zhuǎn)拼接成直角圓形彎管(如圖3)(不計拼接損耗部分),并使得直角圓形彎管的體積最大;
的矩形鐵皮(如圖1)制作成一個直角圓形彎管(如圖3):先在矩形的中間畫一條曲線,并沿曲線剪開,將所得的兩部分分別卷成體積相等的斜截圓柱狀(如圖2),然后將其中一個適當(dāng)翻轉(zhuǎn)拼接成直角圓形彎管(如圖3)(不計拼接損耗部分),并使得直角圓形彎管的體積最大;
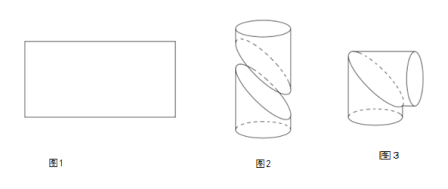
(1)求直角圓形彎管(圖3)的體積;
(2)求斜截面橢圓的焦距;
(3)在相應(yīng)的圖1中建立適當(dāng)?shù)淖鴺?biāo)系,使所畫的曲線的方程為![]() ,求出方程并畫出大致圖像;
,求出方程并畫出大致圖像;
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,矩形![]() 是一個歷史文物展覽廳的俯視圖,點
是一個歷史文物展覽廳的俯視圖,點![]() 在
在![]() 上,在梯形
上,在梯形![]() 區(qū)域內(nèi)部展示文物,
區(qū)域內(nèi)部展示文物,![]() 是玻璃幕墻,游客只能在
是玻璃幕墻,游客只能在![]() 區(qū)域內(nèi)參觀.在
區(qū)域內(nèi)參觀.在![]() 上點
上點![]() 處安裝一可旋轉(zhuǎn)的監(jiān)控攝像頭.
處安裝一可旋轉(zhuǎn)的監(jiān)控攝像頭.![]() 為監(jiān)控角,其中
為監(jiān)控角,其中![]() 、
、![]() 在線段
在線段![]() (含端點)上,且點
(含端點)上,且點![]() 在點
在點![]() 的右下方.經(jīng)測量得知:
的右下方.經(jīng)測量得知:![]() 米,
米,![]() 米,
米,![]() 米,
米,![]() .記
.記![]() (弧度),監(jiān)控攝像頭的可視區(qū)域
(弧度),監(jiān)控攝像頭的可視區(qū)域![]() 的面積為
的面積為![]() 平方米.
平方米.

(1)求![]() 關(guān)于
關(guān)于![]() 的函數(shù)關(guān)系式,并寫出
的函數(shù)關(guān)系式,并寫出![]() 的取值范圍;(參考數(shù)據(jù):
的取值范圍;(參考數(shù)據(jù):![]() )
)
(2)求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某游戲棋盤上標(biāo)有第![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 站,棋子開始位于第
站,棋子開始位于第![]() 站,選手拋擲均勻硬幣進(jìn)行游戲,若擲出正面,棋子向前跳出一站;若擲出反面,棋子向前跳出兩站,直到跳到第
站,選手拋擲均勻硬幣進(jìn)行游戲,若擲出正面,棋子向前跳出一站;若擲出反面,棋子向前跳出兩站,直到跳到第![]() 站或第
站或第![]() 站時,游戲結(jié)束.設(shè)游戲過程中棋子出現(xiàn)在第
站時,游戲結(jié)束.設(shè)游戲過程中棋子出現(xiàn)在第![]() 站的概率為
站的概率為![]() .
.
(1)當(dāng)游戲開始時,若拋擲均勻硬幣![]() 次后,求棋子所走站數(shù)之和
次后,求棋子所走站數(shù)之和![]() 的分布列與數(shù)學(xué)期望;
的分布列與數(shù)學(xué)期望;
(2)證明:![]() ;
;
(3)若最終棋子落在第![]() 站,則記選手落敗,若最終棋子落在第
站,則記選手落敗,若最終棋子落在第![]() 站,則記選手獲勝.請分析這個游戲是否公平.
站,則記選手獲勝.請分析這個游戲是否公平.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]()
(1)若對任意的![]() ,
,![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)若![]() 的最小值為
的最小值為![]() ,求實數(shù)
,求實數(shù)![]() 的值;
的值;
(3)若對任意實數(shù)![]() 、
、![]() 、
、![]() ,均存在以
,均存在以![]() 、
、![]() 、
、![]() 為三邊邊長的三角形,求實數(shù)
為三邊邊長的三角形,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】關(guān)于函數(shù)的對稱性有如下結(jié)論:對于給定的函數(shù)![]() ,如果對于任意的
,如果對于任意的![]() 都有
都有![]() 成立
成立![]() 為常數(shù)),則函數(shù)
為常數(shù)),則函數(shù)![]() 關(guān)于點
關(guān)于點![]() 對稱.
對稱.
(1)用題設(shè)中的結(jié)論證明:函數(shù)![]() 關(guān)于點
關(guān)于點![]() ;
;
(2)若函數(shù)![]() 既關(guān)于點
既關(guān)于點![]() 對稱,又關(guān)于點
對稱,又關(guān)于點![]() 對稱,且當(dāng)
對稱,且當(dāng)![]() 時,
時,![]() ,求:①
,求:①![]() 的值;
的值;
②當(dāng)![]() 時,
時,![]() 的表達(dá)式.
的表達(dá)式.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-4:極坐標(biāo)與參數(shù)方程
已知在平面直角坐標(biāo)系xOy中,O為坐標(biāo)原點,曲線C: 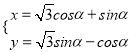 (α為參數(shù)),在以平面直角坐標(biāo)系的原點為極點,x軸的正半軸為極軸,取相同單位長度的極坐標(biāo)系,直線l:ρ
(α為參數(shù)),在以平面直角坐標(biāo)系的原點為極點,x軸的正半軸為極軸,取相同單位長度的極坐標(biāo)系,直線l:ρ![]() .
.
(Ⅰ)求曲線C的普通方程和直線l的直角坐標(biāo)方程;
(Ⅱ)曲線C上恰好存在三個不同的點到直線l的距離相等,分別求出這三個點的極坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】
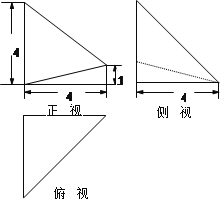
已知幾何體A—BCED的三視圖如圖所示,其中俯視圖和側(cè)視圖都是腰長為4的等腰直角三角形,正視圖為直角梯形.
(1)求此幾何體的體積V的大小;
(2)求異面直線DE與AB所成角的余弦值;
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)f(x)是定義在R 且周期為1的函數(shù),在區(qū)間![]() 上,
上, ![]() 其中集合D=
其中集合D=![]() ,則方程f(x)-lgx=0的解的個數(shù)是____________
,則方程f(x)-lgx=0的解的個數(shù)是____________
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com