
分析 (Ⅰ)由題意,{an}為等比數列,a1=2,2a2+a3=30.即可求出q,可得an;
(Ⅱ)根據bn+1=bn+an,b1=a2,依次遞推計算b2,b3,b4可得b5的值.
解答 解:(Ⅰ)由題意,{an}為等比數列,a1=2,2a2+a3=30.設公比為q,an>0.
可得:4q+2q2=30,
解得:q=3或-5(舍去)
∴an=2•3n-1
(Ⅱ)由b1=a2,
∴b1=2×3=6.
bn+1=bn+an,
∴b2=b1+a1=2+6=8.
b3=b2+a2=8+6=14.
b4=b3+a3=14+18=32.
b5=b4+a4=32+54=86.
點評 本題考查了等比數列的通項公式的求法和根據數列的遞推公式寫出數列的前幾項.屬于基礎題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:解答題
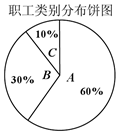 某保險公司針對一個擁有20000人的企業推出一款意外險產品,每年每位職工只要交少量保費,發生意外后可一次性獲得若干賠償金.保險公司把企業的所有崗位共分為A、B、C三類工種,從事三類工種的人數分布比例如圖,根據歷史數據統計出三類工種的賠付頻率如下表(并以此估計賠付頻率).
某保險公司針對一個擁有20000人的企業推出一款意外險產品,每年每位職工只要交少量保費,發生意外后可一次性獲得若干賠償金.保險公司把企業的所有崗位共分為A、B、C三類工種,從事三類工種的人數分布比例如圖,根據歷史數據統計出三類工種的賠付頻率如下表(并以此估計賠付頻率).| 工種類別 | A | B | C |
| 賠付頻率 | $\frac{1}{1{0}^{5}}$ | $\frac{2}{1{0}^{5}}$ | $\frac{1}{1{0}^{4}}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
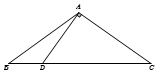 如圖,在△ABC中,已知點D在BC邊上,AD⊥AC,AB=2$\sqrt{5}$,sin∠BAC=$\frac{{\sqrt{5}}}{3}$,AD=3,則BD的長為3.
如圖,在△ABC中,已知點D在BC邊上,AD⊥AC,AB=2$\sqrt{5}$,sin∠BAC=$\frac{{\sqrt{5}}}{3}$,AD=3,則BD的長為3.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | nn | B. | n2 | C. | 2n | D. | n |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,長方體ABCD-A1B1C1D1中,點M在棱BB1上,兩條直線MA,MC與平面ABCD所成角均為θ,AC與BD交于點O.
如圖,長方體ABCD-A1B1C1D1中,點M在棱BB1上,兩條直線MA,MC與平面ABCD所成角均為θ,AC與BD交于點O.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com