【題目】通過隨機詢問100名性別不同的大學生是否愛好踢毽子，得到如下的列聯表：
隨機變量
經計算，統計量K2的觀測值k0≈4.762，參照附表，得到的正確結論是( )
A. 在犯錯誤的概率不超過5%的前提下，認為“愛好該項運動與性別有關”
B. 在犯錯誤的概率不超過5%的前提下，認為“愛好該項運動與性別無關”
C. 有97.5%以上的把握認為“愛好該項運動與性別有關”
D. 有97.5%以上的把握認為“愛好該項運動與性別無關”
學練快車道快樂假期寒假作業系列答案
新思維寒假作業系列答案科目：高中數學 來源： 題型：
【題目】假設關于某種設備的使用年限
(年)與所支出的維修費用
(萬元)有如下統計：
| 2 | 3 | 4 | 5 | 6 |
| 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
已知
， 
. 
， 
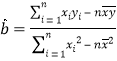(1)求
， 
；
(2)與具有線性相關關系，求出線性回歸方程；
(3)估計使用年限為10年時，維修費用約是多少？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系
中，曲線
的參數方程為
（
為參數），其中
.以原點為極點， 
軸正半軸為極軸建立極坐標系，曲線
的極坐標方程為
.
（1）求出曲線
的普通方程和曲線
的直角坐標方程；
（2）已知曲線
與
交于
， 
兩點，記點
， 
相應的參數分別為
， 
，當
時，求
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f(x)的圖像可以由y=cos2x的圖像先縱坐標不變橫坐標伸長到原來的2倍，再橫坐標不變縱坐標伸長到原來的2倍，最后向右平移
個單位而得到.
⑴求f(x)的解析式與最小正周期；
⑵求f(x)在x∈(0，π)上的值域與單調性.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某公司生產一種產品，第一年投入資金1000萬元，出售產品收入40萬元，預計以后每年的投入資金是上一年的一半，出售產品所得收入比上一年多80萬元，同時，當預計投入的資金低于20萬元時，就按20萬元投入，且當年出售產品收入與上一年相等.
（1）求第
年的預計投入資金與出售產品的收入；
（2）預計從哪一年起該公司開始盈利？（注：盈利是指總收入大于總投入）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，曲線
的參數方程為
(
為參數），以
為極點， 
軸的非負半軸為極軸的極坐標系中，直線
的極坐標方程為
.
（1）求曲線
的極坐標方程；
（2）設直線
與曲線
相交于
兩點，求
的值.
【答案】（1）曲線
的極坐標方程為： 
；（2）6.
【解析】試題分析：（1）先根據三角函數平方關系消參數得曲線
的普通方程，再根據
化為極坐標方程；（2）將直線l的極坐標方程代入曲線
的極坐標方程得
，再根據
求
的值．
試題解析：解:（1）將方程
消去參數
得
，
∴曲線
的普通方程為
，
將
代入上式可得
，
∴曲線
的極坐標方程為： 
． -
（2）設
兩點的極坐標方程分別為
,
由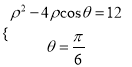
消去
得
，
根據題意可得
是方程
的兩根，
∴
，
∴
．
【題型】解答題
【結束】
23
【題目】選修4—5：不等式選講
已知函數
．
(1)當
時，求關于x的不等式
的解集；
(2)若關于x的不等式
有解，求a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
是公差不為零的等差數列，滿足
，且
、
、
成等比數列.
（1）求數列
的通項公式；
（2）設數列
滿足
，求數列
的前
項和
.
【答案】（1）
；（2）
【解析】試題分析：（1）設等差數列
的公差為
，由a3=7，且
、
、
成等比數列．可得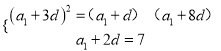
，解之得即可得出數列
的通項公式；
2）由（1）得
，則
，由裂項相消法可求數列
的前
項和
.
試題解析：（1）設數列
的公差為
，且
由題意得
，
即
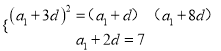，解得
，
所以數列
的通項公式
.
（2）由（1）得
，
.
【題型】解答題
【結束】
18
【題目】四棱錐
的底面
為直角梯形，
，
，
，
為正三角形.
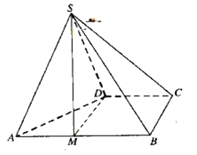
（1）點
為棱
上一點，若
平面
，
，求實數
的值；
（2）求點B到平面SAD的距離.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
