
分析 (1)運用正弦定理和三角形的內角和定理可得cosB,即可得sinB的值.
(2)由BD=1,運用向量的關系可得|$\overrightarrow{BA}+\overrightarrow{BC}$|=2|$\overrightarrow{BD}$|=2,平方后,可得|$\overrightarrow{BA}$|2+|$\overrightarrow{BC}$|2+2$\overrightarrow{BA}•\overrightarrow{BC}$=4利用基本不等式即可求解△ABD面積的最大值.
解答 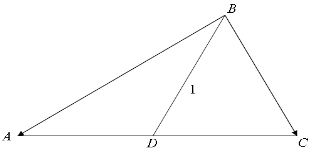 解:(1)由$\frac{b}{a}cosC=({3-\frac{c}{a}})cosB$.
解:(1)由$\frac{b}{a}cosC=({3-\frac{c}{a}})cosB$.
可得:$\frac{b}{a}cosC+\frac{c}{a}cosB=3cosB$
由正弦定理:$\frac{sinBcosC+sinCcosB}{sinA}=3cosB$.
得:$\frac{sinA}{sinA}=3cosB$.即cosB=$\frac{1}{3}$.
那么:sinB=$\frac{2\sqrt{2}}{3}$.
(2)由BD=1,運用向量的關系,可得|$\overrightarrow{BA}+\overrightarrow{BC}$|=2|$\overrightarrow{BD}$|=2,
可得:|$\overrightarrow{BA}$|2+|$\overrightarrow{BC}$|2+2$\overrightarrow{BA}•\overrightarrow{BC}$=4,
則|$\overrightarrow{BA}$|2+|$\overrightarrow{BC}$|2+2|$\overrightarrow{BA}|•|\overrightarrow{BC}$|cosB=4,
由余弦定理:得|$\overrightarrow{BA}$|2+|$\overrightarrow{BC}$|2=4-$\frac{2}{3}$×|$\overrightarrow{BA}|•|\overrightarrow{BC}$|
∵|$\overrightarrow{BA}$|2+|$\overrightarrow{BC}$|2≥2|$\overrightarrow{BA}$|•|$\overrightarrow{BC}$|,(當且僅當|$\overrightarrow{BA}$|=|$\overrightarrow{BC}$|時取等號)
∴4-$\frac{2}{3}$×|$\overrightarrow{BA}|•|\overrightarrow{BC}$|≥2|$\overrightarrow{BA}$|•|$\overrightarrow{BC}$|,
∴|$\overrightarrow{BA}$|•|$\overrightarrow{BC}$|≤$\frac{3}{2}$.
∴△ABC面積S=$\frac{1}{2}$|$\overrightarrow{BA}$|•|$\overrightarrow{BC}$|sinB≤$\frac{1}{2}×\frac{3}{2}×\frac{2\sqrt{2}}{3}$=$\frac{\sqrt{2}}{2}$
那么:△ABD面積的最大值為$\frac{\sqrt{2}}{2}×\frac{1}{2}$=$\frac{\sqrt{2}}{4}$.
點評 本題考查三角形的正余弦定理和內角和定理的運用,基本不等式的靈活運用,考查運算能力,屬于中檔題.


 特高級教師點撥系列答案
特高級教師點撥系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $-\frac{3}{2}i$ | B. | $\frac{1}{2}i$ | C. | $-\frac{3}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
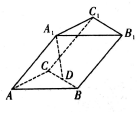 如圖,在三棱柱ABC-A1B1C1中,底面ABC是邊長為2的等邊三角形,點A1在底面ABC上的投影D恰好為BC的中點,AA1與平面ABC所成角為45°,則該三棱柱的體積為( )
如圖,在三棱柱ABC-A1B1C1中,底面ABC是邊長為2的等邊三角形,點A1在底面ABC上的投影D恰好為BC的中點,AA1與平面ABC所成角為45°,則該三棱柱的體積為( )| A. | 1 | B. | $\sqrt{2}$ | C. | 3 | D. | $\sqrt{10}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com