
【題目】已知下列四個命題:
①等差數列一定是單調數列;
②等差數列的前![]() 項和構成的數列一定不是單調數列;
項和構成的數列一定不是單調數列;
③已知等比數列![]() 的公比為
的公比為![]() ,若
,若![]() ,則數列
,則數列![]() 是單調遞增數列.
是單調遞增數列.
④記等差數列的前![]() 項和為
項和為![]() ,若
,若![]() ,
,![]() ,則數列
,則數列![]() 的最大值一定在
的最大值一定在![]() 處達到.
處達到.
其中正確的命題有_____.(填寫所有正確的命題的序號)
【答案】④
【解析】
①舉反例,d=0時為常數列,即可判斷出結論;②舉反例:Sn=n2﹣2n,為單調遞增數列;③舉反例:例如﹣1,﹣2,﹣4,……,為單調遞減數列.④記等差數列的前n項和為Sn,由S2k=k(ak+ak+1)>0,S2k+1=(2k+1)ak+1<0,可得:ak>0,ak+1<0,即可判斷出正誤.
①等差數列不一定是單調數列,例如![]() 時為常數列;
時為常數列;
②等差數列的前![]() 項和構成的數列一定不是單調數列,不正確,反例:
項和構成的數列一定不是單調數列,不正確,反例:![]() ,為單調遞增數列;
,為單調遞增數列;
③已知等比數列![]() 的公比為
的公比為![]() ,若
,若![]() ,則數列
,則數列![]() 是單調遞增數列,不正確,例如-1,-2,-4,……,為單調遞減數列.
是單調遞增數列,不正確,例如-1,-2,-4,……,為單調遞減數列.
④記等差數列的前![]() 項和為
項和為![]() ,
,
若![]() ,
,![]() ,
,
可得:![]() ,
,![]() ,可得數列
,可得數列![]() 的最大值一定在
的最大值一定在![]() 處達到.正確.
處達到.正確.
故答案為:④.


科目:高中數學 來源: 題型:
【題目】隨著經濟模式的改變,微商和電商已成為當今城鄉一種新型的購銷平臺.已知經銷某種商品的電商在任何一個銷售季度內,沒售出1噸該商品可獲利潤0.5萬元,未售出的商品,每1噸虧損0.3萬元.根據往年的銷售經驗,得到一個銷售季度內市場需求量的頻率分布直方圖如圖所示.已知電商為下一個銷售季度籌備了130噸該商品,現以![]() (單位:噸,
(單位:噸,![]() )表示下一個銷售季度的市場需求量,
)表示下一個銷售季度的市場需求量,![]() (單位:萬元)表示該電商下一個銷售季度內經銷該商品獲得的利潤.
(單位:萬元)表示該電商下一個銷售季度內經銷該商品獲得的利潤.
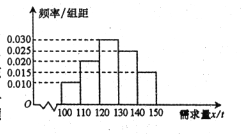
(Ⅰ)視![]() 分布在各區間內的頻率為相應的概率,求
分布在各區間內的頻率為相應的概率,求![]() ;
;
(Ⅱ)將![]() 表示為
表示為![]() 的函數,求出該函數表達式;
的函數,求出該函數表達式;
(Ⅲ)在頻率分布直方圖的市場需求量分組中,以各組的區間中點值(組中值)代表該組的各個值,并以市場需求量落入該區間的頻率作為市場需求量取該組中值的概率(例如![]() ,則取
,則取![]() 的概率等于市場需求量落入
的概率等于市場需求量落入![]() 的頻率),求
的頻率),求![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】李明自主創業,在網上經營一家水果店,銷售的水果中有草莓、京白梨、西瓜、桃,價格依次為60元/盒、65元/盒、80元/盒、90元/盒.為增加銷量,李明對這四種水果進行促銷:一次購買水果的總價達到120元,顧客就少付x元.每筆訂單顧客網上支付成功后,李明會得到支付款的80%.
①當x=10時,顧客一次購買草莓和西瓜各1盒,需要支付__________元;
②在促銷活動中,為保證李明每筆訂單得到的金額均不低于促銷前總價的七折,則x的最大值為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 過點
過點![]() ,其參數方程為
,其參數方程為 (
(![]() 為參數,
為參數, ![]() ),以
),以![]() 為極點,
為極點, ![]() 軸非負半軸為極軸,建立極坐標系,曲線
軸非負半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)求已知曲線![]() 和曲線
和曲線![]() 交于
交于![]() 兩點,且
兩點,且![]() ,求實數
,求實數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() ,
,![]() ,其前
,其前![]() 項和
項和![]() 滿足
滿足![]() ,其中
,其中![]() .
.
(1)設![]() ,證明:數列
,證明:數列![]() 是等差數列;
是等差數列;
(2)設![]() ,
,![]() 為數列
為數列![]() 的前
的前![]() 項和,求證:
項和,求證:![]() ;
;
(3)設![]() (
(![]() 為非零整數,
為非零整數,![]() ),試確定
),試確定![]() 的值,使得對任意
的值,使得對任意![]() ,都有
,都有![]() 成立.
成立.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com