Question

在平面幾何中，有勾股定理：“設△ABC的兩邊AB、AC互相垂直，則AB²＋AC²＝BC².”拓展到空間，類比平面幾何的勾股定理，研究三棱錐的側面面積與底面面積間的關系，可以得出的正確結論是：“設三棱錐A—BCD的三個側面ABC、ACD、ADB兩兩相互垂直，則　　　　　　.”

Answer 1

類比條件：兩邊AB、AC互相垂直，

三棱錐三個側面兩兩垂直，

則AB²＋AC²＝BC²類比S_△ABC²＋S_△ACD²＋S_△ADB²＝S_△BCD².

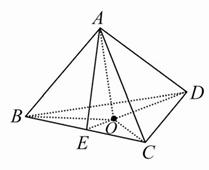證明：如圖，AO⊥平面BCD于點O，由三個側面兩兩互相垂直可知三條側棱AB，AC，AD兩兩互相垂直，故O為三角形BCD的垂心，在Rt△DAE中，AO⊥DE，有AE²＝EO·ED，

S_△ABC²＝BC²·AE²＝(BC·EO)(BC·ED)

＝S_△OBC·S_△BCD，

同理S_△ACD²＝S_△BCD·S_△OCD，S_△ABD²＝S_△BCD·S_△OBD，

故S_△ABC²＋S_△ACD²＋S_△ADB²＝S_△BCD ².

答案：S_△ABC²＋S_△ACD²＋S_△ADB²＝S_△BCD²