【答案】
分析:(1)根據(jù)a
n+2=(1+cos
2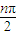
)a
n+sin
2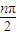
,把a
1和a
2代入即可求得a
3,a
4,先看當n=2k-1(k∈N
*)時,整理得a
2k+1-a
2k-1=1進而可判斷數(shù)列{a
2k-1}是首項為1、公差為1的等差數(shù)列;n=2k(k∈N
*)時,整理得a
2k+2=2a
2k進而可判斷數(shù)列{a
2k}是首項為2、公比為2的等比數(shù)列,最后綜合可得答案.
(2)把(1)中求得a
n代入b
n中可知數(shù)列{b
n}是由等比和等差數(shù)列構(gòu)成,因而可用錯位相減法求和,得到數(shù)列的求和公式S
n=2-
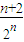
..要證明當n≥6時,|S
n-2|<
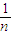
成立,只需證明當n≥6時,
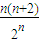
<1成立.用數(shù)學歸納法,先看當n=6時求得
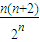
<1,再假設(shè)當n=k(k≥6)時不等式成立,通過n=k+1時,等式亦成立,進而證明結(jié)論.
解答:解:(1)因為a
1=1,a
2=2,
所以a
3=(1+cos
2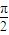
)a
1+sin
2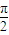
=a
1+1=2,
a
4=(1+cos
2π)a
2+sin
2π=2a
2=4.
一般地,當n=2k-1(k∈N
*)時,a
2k+1=[1+cos
2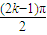
]a
2k-1+sin
2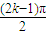
=a
2k-1+1,即a
2k+1-a
2k-1=1.
所以數(shù)列{a
2k-1}是首項為1、公差為1的等差數(shù)列,
因此a
2k-1=k.
當n=2k(k∈N
*)時,a
2k+2=(1+cos
2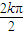
)a
2k+sin
2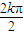
=2a
2k.
所以數(shù)列{a
2k}是首項為2、公比為2的等比數(shù)列,
因此a
2k=2
k.
故數(shù)列{a
n}的通項公式為
a
n=
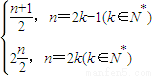
(2)由(1)知,b
n=

=

,
所以S
n=

+
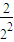
+
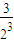
+…+
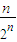
,①

S
n=
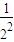
+
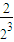
+
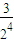
+…+
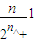
,②
①-②得,

S
n=

+
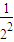
+
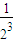
+…+
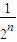
-
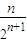
=
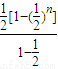
-
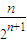
=1-
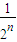
-
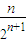
,
所以S
n=2-
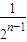
-
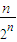
=2-
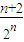
.
要證明當n≥6時,|S
n-2|<
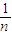
成立,只需證明當n≥6時,
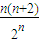
<1成立.
(1)當n=6時,
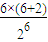
=
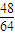
=

<1成立.
(2)假設(shè)當n=k(k≥6)時不等式成立,即
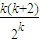
<1.
則當n=k+1時,
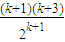
=
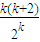
×
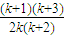
<
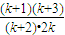
<1.
由(1)、(2)所述,當n≥6時,
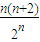
<1.
即當n≥6時,|S
n-2|<
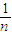
.
點評:本題主要考查了數(shù)列的遞推式.數(shù)列的遞推式常用來解決數(shù)列求通項公式等問題,有時要注意數(shù)列中的奇數(shù)項和偶數(shù)項的不同.

 )an+sin2
)an+sin2 ,n=1,2,3,….
,n=1,2,3,…. ,Sn=b1+b2+…+bn.證明:當n≥6時,|Sn-2|<
,Sn=b1+b2+…+bn.證明:當n≥6時,|Sn-2|< .
.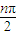 )an+sin2
)an+sin2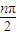 ,把a1和a2代入即可求得a3,a4,先看當n=2k-1(k∈N*)時,整理得a2k+1-a2k-1=1進而可判斷數(shù)列{a2k-1}是首項為1、公差為1的等差數(shù)列;n=2k(k∈N*)時,整理得a2k+2=2a2k進而可判斷數(shù)列{a2k}是首項為2、公比為2的等比數(shù)列,最后綜合可得答案.
,把a1和a2代入即可求得a3,a4,先看當n=2k-1(k∈N*)時,整理得a2k+1-a2k-1=1進而可判斷數(shù)列{a2k-1}是首項為1、公差為1的等差數(shù)列;n=2k(k∈N*)時,整理得a2k+2=2a2k進而可判斷數(shù)列{a2k}是首項為2、公比為2的等比數(shù)列,最后綜合可得答案.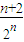 ..要證明當n≥6時,|Sn-2|<
..要證明當n≥6時,|Sn-2|<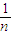 成立,只需證明當n≥6時,
成立,只需證明當n≥6時,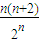 <1成立.用數(shù)學歸納法,先看當n=6時求得
<1成立.用數(shù)學歸納法,先看當n=6時求得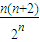 <1,再假設(shè)當n=k(k≥6)時不等式成立,通過n=k+1時,等式亦成立,進而證明結(jié)論.
<1,再假設(shè)當n=k(k≥6)時不等式成立,通過n=k+1時,等式亦成立,進而證明結(jié)論.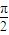 )a1+sin2
)a1+sin2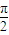 =a1+1=2,
=a1+1=2,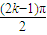 ]a2k-1+sin2
]a2k-1+sin2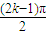 =a2k-1+1,即a2k+1-a2k-1=1.
=a2k-1+1,即a2k+1-a2k-1=1.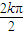 )a2k+sin2
)a2k+sin2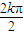 =2a2k.
=2a2k.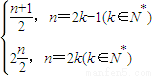
 =
= ,
, +
+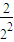 +
+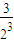 +…+
+…+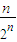 ,①
,① Sn=
Sn=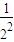 +
+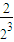 +
+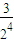 +…+
+…+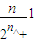 ,②
,② Sn=
Sn= +
+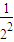 +
+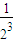 +…+
+…+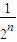 -
-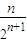 =
=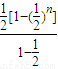 -
-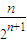 =1-
=1-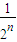 -
-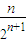 ,
,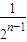 -
-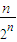 =2-
=2-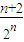 .
.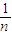 成立,只需證明當n≥6時,
成立,只需證明當n≥6時,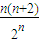 <1成立.
<1成立.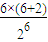 =
=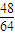 =
= <1成立.
<1成立.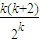 <1.
<1.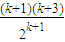 =
=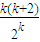 ×
×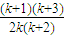 <
<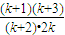 <1.
<1.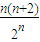 <1.
<1.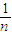 .
.

 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案