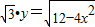日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 高中數學 > 題目詳情
已知點（m，n）在曲線上，則m2+（n-1）2的取值范圍是（ ）
A．[1，2]
B．[1，3]
C．[1，4]
D．[1，9]
【答案】分析：可將兩端平方，化為橢圓方程（上半部分），將（m，n）代入方程，整理只含有n的關系式，利用n的取值范圍即可求得m2+（n-1）2的取值范圍．
解答：解：由兩端平方后整理得：，
又點（m，n）在曲線上，
∴，∴，
∴m2+（n-1）2==（0≤n≤2），
∴，即1≤m2+（n-1）2≤4．
故選C．
點評：本題考查橢圓的簡單性質，著重考查學生的化歸思想及綜合應用知識解決問題的能力，屬于中檔題．
練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

如圖，直線l1和l2相交于點M且l1⊥l2，點N∈l1．以A、B為端點的曲線段C上的任一點到l2的距離與到點N的距離相等．若△AMN為銳角三角形，|AM|=
17
，|AN|=3，且|BN|=6．
（1）曲線段C是哪類圓錐曲線的一部分？并建立適當的坐標系，求曲線段C所在的圓錐曲線的標準方程；
（2）在（1）所建的坐標系下，已知點P（m，n）在曲線段C上，直線l：mx+ny=1，求直線l被圓x2+y2=1截得的弦長的取值范圍．

查看答案和解析>>

科目：高中數學 來源： 題型：

已知焦點在x軸上的雙曲線C的兩條漸近線過坐標原點，且兩條漸近線與以點A (0，)為圓心，1為半徑的圓相切，又知C的一個焦點與A關于y = x對稱．

    （1）求雙曲線C的方程；

    （2）若Q是雙曲線線C上的任一點，F1，F2為雙曲線C的左、右兩個焦點，從F1引∠F1QF2的平分線的垂線，垂足為N，試求點N的軌跡方程；

    （3）設直線y = mx + 1與雙曲線C的左支交于A、B兩點，另一直線l經過M (–2，0)及AB的中點，求直線l在y軸上的截距b的取值范圍．

查看答案和解析>>

科目：高中數學 來源：2011-2012學年福建師大附中高二（上）期末數學試卷（文科）（解析版） 題型：解答題

如圖，直線l1和l2相交于點M且l1⊥l2，點N∈l1．以A、B為端點的曲線段C上的任一點到l2的距離與到點N的距離相等．若△AMN為銳角三角形，，|AN|=3，且|BN|=6．
（1）曲線段C是哪類圓錐曲線的一部分？并建立適當的坐標系，求曲線段C所在的圓錐曲線的標準方程；
（2）在（1）所建的坐標系下，已知點P（m，n）在曲線段C上，直線l：mx+ny=1，求直線l被圓x2+y2=1截得的弦長的取值范圍．

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 国产无毛 | www.99热| 超碰人人搞 | 国产中文在线 | 开心激情站 | 日韩成人在线观看 | 精品国产三级a在线观看 | 日韩中文字幕国产 | 九九免费视频 | 欧美日韩一区二区视频在线观看 | 国产激情精品视频 | 亚洲不卡视频在线 | 国产精品成人国产乱一区 | 91精品久久久久久久久中文字幕 | 欧美成人精品一区二区男人看 | 久久久网 | 久久噜噜噜精品国产亚洲综合 | 天天添夜夜操 | 日韩久久综合 | 午夜精品网站 | 中文字幕免费看 | 亚洲清色 | 精品久久久久一区二区三区 | 国产一区二区高清视频 | 亚洲欧美一区二区三区在线 | 中文字幕免费在线 | 日韩视频在线观看一区 | 91亚洲日本 | 色欧美综合 | 久久国产一区二区 | 成人久久久精品乱码一区二区三区 | 国产区精品在线 | 亚洲一区在线观看视频 | 日本a在线 | 久久精品久久久 | 久久av一区二区三区 | 亚洲一级免费视频 | 绯色av一区二区三区在线高清 | 激情国产 | 亚洲区视频 | 伊人久久国产 |