
| A. | $m≤\frac{3}{2}\;,\;\;n=\frac{5}{2}$ | B. | m≤3,n=2 | C. | $m>\frac{3}{2}$ | D. | m>3,n=2 |
分析 曲線$y=msin\frac{ω}{2}x+n({m>0\;,\;\;n>0})$的性質知,在一個周期上截直線y=5與y=-1所得的弦長相等且不為0,可知兩條直線關于y=n對稱,由此對稱性可求出n,又截得的弦長不為0,故可得振幅大于 3.
解答 解:由題意可得$y=msin\frac{ω}{2}x+n({m>0\;,\;\;n>0})$的圖象關于直線y=n對稱,
因為曲線被直線y=5與y=-1所得的弦長相等,
所以直線y=5與直線y=-1關于y=n對稱.
所以n=$\frac{5-1}{2}$=2,
又因為弦長相等且不為0,
所以振幅m>$\frac{5+1}{2}$=3.
故選D.
點評 本題考點y=Asin(ωx+φ)中參數的物理意義,考查三角函數的圖象的性質及其與相應參數的關系,考查對三角函數圖象的特征理解的能力.


 一本好題口算題卡系列答案
一本好題口算題卡系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{7}$ | B. | -$\frac{1}{5}$ | C. | $\frac{1}{5}$ | D. | -$\frac{1}{7}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
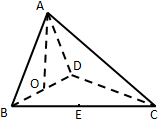 如圖,四面體ABCD中,O、E分別為BD、BC的中點,且CA=CB=CD=BD=$\sqrt{2}$,AB=AD=1,則異面直線AB與CD所成角的正切值為.( )
如圖,四面體ABCD中,O、E分別為BD、BC的中點,且CA=CB=CD=BD=$\sqrt{2}$,AB=AD=1,則異面直線AB與CD所成角的正切值為.( )| A. | $\sqrt{7}$ | B. | $\frac{\sqrt{7}}{8}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$](k∈Z) | B. | [kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$](k∈Z) | ||
| C. | [kπ+$\frac{π}{12}$,kπ+$\frac{7π}{12}$](k∈Z) | D. | [kπ-$\frac{5π}{12}$,kπ+$\frac{π}{12}$](k∈Z) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\left.\begin{array}{l}{α⊥γ}\\{β⊥γ}\end{array}\right\}$⇒α∥β | B. | $\left.\begin{array}{l}{m⊥l}\\{n⊥l}\end{array}\right\}$⇒m∥n | C. | $\left.\begin{array}{l}{m∥β}\\{l⊥m}\end{array}\right\}$⇒l∥β | D. | $\left.\begin{array}{l}{m∥n}\\{n⊥γ}\end{array}\right\}$⇒m⊥γ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com