
【題目】已知函數![]() .
.
(1)若函數![]() 在定義域上是單調增函數,求實數a的取值范圍;
在定義域上是單調增函數,求實數a的取值范圍;
(2)討論![]() 的極值點的個數;
的極值點的個數;
(3)若![]() 有兩個極值點
有兩個極值點![]() ,且
,且![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)當
;(2)當![]() 時,
時,![]() 的極值點的個數為0;當
的極值點的個數為0;當![]() 時,
時,![]() 的極值點的個數為2;(3)
的極值點的個數為2;(3)![]()
【解析】
(1)求出導函數![]() ,題意說明
,題意說明![]() 在
在![]() 上恒成立,可用分離參數法轉化為求函數最值(可用基本不等式求最值).
上恒成立,可用分離參數法轉化為求函數最值(可用基本不等式求最值).
(2)由![]() ,對
,對![]() 分類討論,在(1)的基礎上,
分類討論,在(1)的基礎上,![]() 時無極值點,在
時無極值點,在![]() 時,求出
時,求出![]() 的兩根,可列表得出
的兩根,可列表得出![]() 的正負,得
的正負,得![]() 的單調性,從而得極值點.
的單調性,從而得極值點.
(3)由(2)知![]() ,
,![]() ,求出
,求出![]() ,注意
,注意![]() 代換后可轉化為
代換后可轉化為![]() 的代數式,令
的代數式,令![]() ,首先有
,首先有![]() ,
,![]() 變為
變為![]() 的函數,由
的函數,由![]() 求出
求出![]() 的取值范圍后可得
的取值范圍后可得![]() 的取值范圍.
的取值范圍.
解:(1)定義域為![]() ,由題意得
,由題意得![]()
因為函數![]() 在定義域上是單調增函數,所以
在定義域上是單調增函數,所以![]() 在
在![]() 上恒成立
上恒成立
因為![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 上恒成立
上恒成立
因為![]() ,當且僅當
,當且僅當![]() 時取等號,
時取等號,
所以![]() ,即
,即![]() ,所以,實數a的取值范圍為
,所以,實數a的取值范圍為![]()
(2)![]() ,
,
①![]() 時,由第(1)問可知,函數
時,由第(1)問可知,函數![]() 在定義域上是單調增函數;
在定義域上是單調增函數;
所以![]() 無極值點,即
無極值點,即![]() 的極值點的個數為0
的極值點的個數為0
②![]() 時,令
時,令![]() ,得:
,得:![]() ,
,![]()
當![]() 時,
時,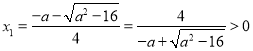 ,故
,故![]()
列表:
|
|
|
|
|
|
| + | 0 | - | 0 | + |
|
| 極大值 |
| 極小值 |
|
當![]() 時,
時,![]() 有極大值,當
有極大值,當![]() 時,
時,![]() 有極小值
有極小值
所以,![]() 的極值點的個數為2
的極值點的個數為2
綜上所述,當![]() 時,
時,![]() 的極值點的個數為0;當
的極值點的個數為0;當![]() 時,
時,![]() 的極值點的個數為2
的極值點的個數為2
(3)由題意知,![]() ,
,
因為![]() 是函數
是函數![]() 的兩個極值點,所以是方程
的兩個極值點,所以是方程![]() 的兩個不等實根
的兩個不等實根
所以![]() ,
,![]()
所以![]()
![]()
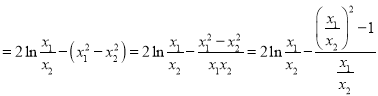
令![]() ,記
,記![]()
由![]() 可得:
可得:![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以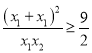 ,所以
,所以![]() ,即
,即![]() ,
,
因為![]() ,解得:
,解得:![]()
又![]() ,所以
,所以![]() 在
在![]() 上單調減
上單調減
所以![]()
所以![]() 的最小值為
的最小值為![]()


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】總體由編號為01,02,03,![]() ,49,50的50個個體組成,利用隨機數表(以下選取了隨機數表中的第1行和第2行)選取5個個體,選取方法是從隨機數表第1行的第9列和第10列數字開始由左向右讀取,則選出來的第4個個體的編號為( )
,49,50的50個個體組成,利用隨機數表(以下選取了隨機數表中的第1行和第2行)選取5個個體,選取方法是從隨機數表第1行的第9列和第10列數字開始由左向右讀取,則選出來的第4個個體的編號為( )
78 16 65 72 08 02 63 14 07 02 43 69 69 38 74 |
32 04 94 23 49 55 80 20 36 35 48 69 97 28 01 |
A. 05 B. 09 C. 07 D. 20
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量![]() ,
,![]() 函數
函數![]() .
.
(1)將函數![]() 的圖像向右平移m(
的圖像向右平移m(![]() )個單位長度,所得圖像對應的函數為奇函數,寫出m的最小值(不要求寫過程);
)個單位長度,所得圖像對應的函數為奇函數,寫出m的最小值(不要求寫過程);
(2)若![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)若函數![]() (
(![]() )在區間
)在區間![]() 上是單調遞增函數,求正數
上是單調遞增函數,求正數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 是定義在R上的奇函數,且滿足
是定義在R上的奇函數,且滿足![]() ,
,![]() =1,數列{
=1,數列{![]() }滿足
}滿足![]() =﹣1,
=﹣1, ![]() (
(![]() ),其中
),其中![]() 是數列{
是數列{![]() }的前n項和,則
}的前n項和,則![]() =
=
A. ﹣2 B. ﹣1 C. 0 D. 1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,曲線![]() :
:![]() =0(a>0),曲線
=0(a>0),曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以坐標原點O為極點,x軸正半軸為極軸建立極坐標系;
為參數),以坐標原點O為極點,x軸正半軸為極軸建立極坐標系;
(1)求曲線![]() ,
,![]() 的極坐標方程;
的極坐標方程;
(2)已知極坐標方程為![]() =
=![]() 的直線與曲線
的直線與曲線![]() ,
,![]() 分別相交于P,Q兩點(均異于原點O),若|PQ|=
分別相交于P,Q兩點(均異于原點O),若|PQ|=![]() ﹣1,求實數a的值;
﹣1,求實數a的值;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數![]() 同時滿足:①對于定義域上的任意
同時滿足:①對于定義域上的任意![]() ,恒有
,恒有![]() ;②對于定義域上的任意
;②對于定義域上的任意![]() ,當
,當![]() 時,恒有
時,恒有![]() ,則稱函數
,則稱函數![]() 為“理想函數”.給出下列四個函數中:①
為“理想函數”.給出下列四個函數中:① ![]() ; ②
; ②![]() ; ③
; ③![]() ; ④
; ④ 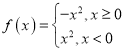 ,能被稱為“理想函數”的有_____(請將所有正確命題的序號都填上).
,能被稱為“理想函數”的有_____(請將所有正確命題的序號都填上).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了適應高考改革,某中學推行“創新課堂”教學.高一平行甲班采用“傳統教學”的教學方式授課,高一平行乙班采用“創新課堂”的教學方式授課,為了比較教學效果,期中考試后,分別從兩個班中各隨機抽取![]() 名學生的成績進行統計分析,結果如下表:(記成績不低于
名學生的成績進行統計分析,結果如下表:(記成績不低于![]() 分者為“成績優秀”)
分者為“成績優秀”)
分數 |
|
|
|
|
|
|
|
甲班頻數 |
|
|
|
|
|
|
|
乙班頻數 |
|
|
|
|
|
|
|
(1)由以上統計數據填寫下面的![]() 列聯表,并判斷是否有
列聯表,并判斷是否有![]() 以上的把握認為“成績優秀與教學方式有關”?
以上的把握認為“成績優秀與教學方式有關”?
甲班 | 乙班 | 總計 | |
成績優秀 | |||
成績不優秀 | |||
總計 |
(2)在上述樣本中,學校從成績為![]() 的學生中隨機抽取
的學生中隨機抽取![]() 人進行學習交流,求這
人進行學習交流,求這![]() 人來自同一個班級的概率.
人來自同一個班級的概率.
參考公式:![]() ,其中
,其中![]() .
.
臨界值表
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() ).
).
(1)若函數![]() 在區間
在區間![]() 上的最小值為1,求實數m的值;
上的最小值為1,求實數m的值;
(2)若函數![]() ,其中
,其中![]() 為奇函數,
為奇函數,![]() 為偶函數,不等式
為偶函數,不等式![]() 對任意
對任意![]() 恒成立,求實數a的取值范圍.
恒成立,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com