
【題目】已知函數![]() ,
,![]() .
.
(1)若不等式![]() 對
對![]() 恒成立,求
恒成立,求![]() 的最小值;
的最小值;
(2)證明:![]() .
.
(3)設方程![]() 的實根為
的實根為![]() .令
.令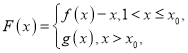 若存在
若存在![]() ,
,![]() ,
,![]() ,使得
,使得![]() ,證明:
,證明:![]() .
.
【答案】(1)![]() (2)證明見解析(3)證明見解析
(2)證明見解析(3)證明見解析
【解析】
(1)由題意可得,![]() ,令
,令![]() ,利用導數得
,利用導數得![]() 在
在![]() 上單調遞減,進而可得結論;
上單調遞減,進而可得結論;
(2)不等式轉化為![]() ,令
,令![]() ,
,![]() ,利用導數得單調性即可得到答案;
,利用導數得單調性即可得到答案;
(3)由題意可得![]() ,進而可將不等式轉化為
,進而可將不等式轉化為![]() ,再利用單調性可得
,再利用單調性可得![]() ,記
,記![]() ,
,![]() ,再利用導數研究單調性可得
,再利用導數研究單調性可得![]() 在
在![]() 上單調遞增,即
上單調遞增,即![]() ,即
,即![]() ,即可得到結論.
,即可得到結論.
(1)![]() ,即
,即![]() ,化簡可得
,化簡可得![]() .
.
令![]() ,
,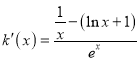 ,因為
,因為![]() ,所以
,所以![]() ,
,![]() .
.
所以![]() ,
,![]() 在
在![]() 上單調遞減,
上單調遞減,![]() .
.
所以![]() 的最小值為
的最小值為![]() .
.
(2)要證![]() ,即
,即![]() .
.
兩邊同除以![]() 可得
可得![]() .
.
設![]() ,則
,則![]() .
.
在![]() 上,
上,![]() ,所以
,所以![]() 在
在![]() 上單調遞減.
上單調遞減.
在![]() 上,
上,![]() ,所以
,所以![]() 在
在![]() 上單調遞增,所以
上單調遞增,所以![]() .
.
設![]() ,因為
,因為![]() 在
在![]() 上是減函數,所以
上是減函數,所以![]() .
.
所以![]() ,即
,即![]() .
.
(3)證明:方程![]() 在區間
在區間![]() 上的實根為
上的實根為![]() ,即
,即![]() ,要證
,要證
![]() ,由
,由![]() 可知,即要證
可知,即要證![]() .
.
當![]() 時,
時,![]() ,
,![]() ,因而
,因而![]() 在
在![]() 上單調遞增.
上單調遞增.
當![]() 時,
時,![]() ,
,![]() ,因而
,因而![]() 在
在![]() 上單調遞減.
上單調遞減.
因為![]() ,所以
,所以![]() ,要證
,要證![]() .
.
即要證![]() .
.
記![]() ,
,![]() .
.
因為![]() ,所以
,所以![]() ,則
,則![]() .
.
![]() .
.
設![]() ,
,![]() ,當
,當![]() 時,
時,![]() .
.
![]() 時,
時,![]() ,故
,故![]() .
.
且![]() ,故
,故![]() ,因為
,因為![]() ,所以
,所以![]() .
.
因此![]() ,即
,即![]() 在
在![]() 上單調遞增.
上單調遞增.
所以![]() ,即
,即![]() .
.
故![]() 得證.
得證.


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:高中數學 來源: 題型:
【題目】某醫院體檢中心為回饋大眾,推出優惠活動:對首次參加體檢的人員,按200元次收費,并注冊成為會員,對會員的后續體檢給予相應優惠,標準如下:
體檢次序 | 第一次 | 第二次 | 第三次 | 第四次 | 第五次及以上 |
收費比例 | 1 | 0.95 | 0.90 | 0.85 | 0.8 |
該體檢中心從所有會員中隨機選取了100位對他們在本中心參加體檢的次數進行統計,得到數據如下表:
體檢次數 | 一次 | 兩次 | 三次 | 四次 | 五次及以上 |
頻數 | 60 | 20 | 10 | 5 | 5 |
假設該體檢中心為顧客體檢一次的成本費用為150元,根據所給數據,解答下列問題:
(1)該體檢中心要從這100人里至少體檢3次的會員中,按體檢次數用分層抽樣的方法抽出8人,再從這8人中抽出2人發放紀念品,求抽出的2人中恰有1人體檢3次的概率;
(2)若以這100位會員體檢次數的頻率分布估計該體檢中心所有會員體檢次數的概率分布,已知該中心本周共接待了1000名顧客參加體檢,試估計該體檢中心本周所獲利潤.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,四邊形
中,四邊形![]() 是邊長為2的正方形,
是邊長為2的正方形,![]() ,
,![]() 為
為![]() 的中點,點
的中點,點![]() 在
在![]() 上,
上,![]() 平面
平面![]() ,
,![]() 在
在![]() 的延長線上,且
的延長線上,且![]() .
.
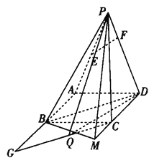
(1)證明:![]() 平面
平面![]() .
.
(2)過點![]() 作
作![]() 的平行線,與直線
的平行線,與直線![]() 相交于點
相交于點![]() ,點
,點![]() 為
為![]() 的中點,求
的中點,求![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知長方形![]() 中,
中,![]() ,
,![]() ,現將長方形沿對角線
,現將長方形沿對角線![]() 折起,使
折起,使![]() ,得到一個四面體
,得到一個四面體![]() ,如圖所示.
,如圖所示.
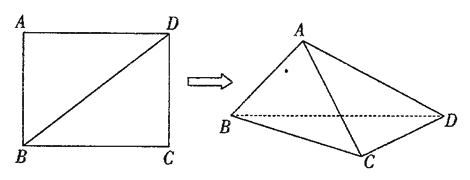
(1)試問:在折疊的過程中,異面直線![]() 與
與![]() 能否垂直?若能垂直,求出相應的
能否垂直?若能垂直,求出相應的![]() 的值;若不垂直,請說明理由;
的值;若不垂直,請說明理由;
(2)當四面體![]() 體積最大時,求二面角
體積最大時,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設三棱錐![]() 的每個頂點都在球
的每個頂點都在球![]() 的球面上,
的球面上,![]() 是面積為
是面積為![]() 的等邊三角形,
的等邊三角形,![]() ,
,![]() ,且平面
,且平面![]() 平面
平面![]() .
.
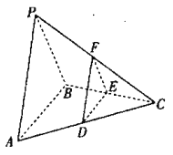
(1)確定![]() 的位置(需要說明理由),并證明:平面
的位置(需要說明理由),并證明:平面![]() 平面
平面![]() .
.
(2)與側面![]() 平行的平面
平行的平面![]() 與棱
與棱![]() ,
,![]() ,
,![]() 分別交于
分別交于![]() ,
,![]() ,
,![]() ,求四面體
,求四面體![]() 的體積的最大值.
的體積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com