
【題目】如圖所示,正三角形![]() 所在平面與梯形
所在平面與梯形![]() 所在平面垂直,
所在平面垂直, ![]() ,
, ![]() ,
, ![]() 為棱
為棱![]() 的中點.
的中點.
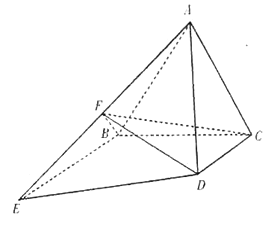
(1)求證: ![]() 平面
平面![]() ;
;
(2)求證: ![]() 平面
平面![]() ;
;
(3)若直線![]() 與平面
與平面![]() 所成角的正切值為
所成角的正切值為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)見解析(2)見解析(3)![]()
【解析】【試題分析】(1)運用線面平行的判定定理進行推證;(2)依據題設運用線面垂直的判定定理進行推證;(3)先建立空間直角坐標系,再運用向量的數量積工具進行求解:
(1)如圖,取![]() 中點
中點![]() ,連接
,連接![]() ,因為
,因為![]() 為
為![]() 中點,所以
中點,所以![]() 且
且![]() ,
, ![]() ,所以
,所以![]() 且
且![]() ,所以四邊形
,所以四邊形![]() 為平行四邊形,所以
為平行四邊形,所以![]() .
.
![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)又因為![]() 為正三角形,所以
為正三角形,所以![]() ,
,
又因為面![]() 面
面![]() ,面
,面![]() 面
面![]() .
. ![]() 面
面![]() ,
,
所以![]() 面
面![]() ,
, ![]() .又因為
.又因為![]() ,所以
,所以![]() 面
面![]() ,所以
,所以![]() 面
面![]() .
.
(3)
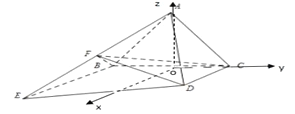
取![]() 中點
中點![]() ,再連接
,再連接![]() .易證
.易證![]() 面
面![]() ,所以
,所以![]() 為直線
為直線![]() 與平面
與平面![]() 所成的角,即
所成的角,即![]() ,設
,設![]() ,可求得
,可求得![]() .
.
以![]() 為原點,建立如圖所示的空間直角坐標系
為原點,建立如圖所示的空間直角坐標系![]() ,則
,則![]() ,
, ![]() ,
, 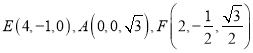 ,
,
所以 ,
,
設平面![]() 的法向量為
的法向量為![]() ,則
,則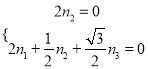 ,令
,令![]() ,得
,得
![]() ,所以
,所以![]() ,
,
設面![]() 的法向量為
的法向量為![]() ,則
,則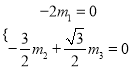 ,令
,令![]() ,得
,得![]() ,
, ![]() ,
,
所以![]() ,所以
,所以 ,
,
因為二面角![]() 為鈍角,其余弦值為
為鈍角,其余弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ex﹣1,g(x)=﹣x2+4x﹣3,若有f(a)=g(b),則b的取值范圍為( )
A.![]()
B.(2﹣ ![]() ,2+
,2+ ![]() )
)
C.[1,3]
D.(1,3)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,AB=2,點E、F分別在邊AB、DC上,M為AD的中點,且 ![]() =0,則△MEF的面積的取值范圍為( )
=0,則△MEF的面積的取值范圍為( ) 
A.![]()
B.[1,2]
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某車間共有![]() 名工人,隨機抽取6名,他們某日加工零件個數的莖葉圖如圖所示,其中莖為十位數,葉為個位數.
名工人,隨機抽取6名,他們某日加工零件個數的莖葉圖如圖所示,其中莖為十位數,葉為個位數.

(Ⅰ) 根據莖葉圖計算樣本均值;
(Ⅱ) 日加工零件個數大于樣本均值的工人為優秀工人,根據莖葉圖推斷該車間![]() 名工人中有幾名優秀工人;
名工人中有幾名優秀工人;
(Ⅲ) 從該車間![]() 名工人中,任取2人,求恰有1名優秀工人的概率.
名工人中,任取2人,求恰有1名優秀工人的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下表是某校高三一次月考5個班級的數學、物理的平均成績:
班級 | 1 | 2 | 3 | 4 | 5 |
數學( | 111 | 113 | 119 | 125 | 127 |
物理( | 92 | 93 | 96 | 99 | 100 |
(Ⅰ)一般來說,學生的物理成績與數學成績具有線性相關關系,根據上表提供的數據,求兩個變量![]() ,
, ![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(Ⅱ)從以上5個班級中任選兩個參加某項活動,設選出的兩個班級中數學平均分在115分以上的個數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
附:  ,
, ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com