Question

【題目】如圖，小華和小明兩個小伙伴在一起做游戲，他們通過劃拳（剪刀、石頭、布）比賽決勝誰首先登上第3個臺階，他們規定從平地開始，每次劃拳贏的一方登上一級臺階，輸的一方原地不動，平局時兩個人都上一級臺階，如果一方連續兩次贏，那么他將額外獲得一次上一級臺階的獎勵，除非已經登上第3個臺階，當有任何一方登上第3個臺階時，游戲結束，記此時兩個小伙伴劃拳的次數為．

（1）求游戲結束時小華在第2個臺階的概率；

（2）求的分布列和數學期望．

Answer 1

【答案】（1）（2）

【解析】試題分析：（1）根據等可能性知每次贏、平、輸的概率皆為．再分兩種情況分別計數：一種是小華在第1個臺階，并且小明在第2個臺階，最后一次劃拳小華平；另一種是小華在第2個臺階，并且小明也在第2個臺階，最后一次劃拳小華輸，逆推確定事件數及對應劃拳的次數，最后利用互斥事件概率加法公式求概率，（2）先確定隨機變量取法,再分別利用組合求對應概率,列表可得分布列,最后根據數學期望公式求期望.

試題解析：解：（1）易知對于每次劃拳比賽基本事件共有個，其中小華贏（或輸）包含三個基本事件上，他們平局也為三個基本事件，不妨設事件“第次劃拳小華贏”為；事件“第 次劃拳小華平”為；事件“第 次劃拳小華輸”為，所以．

因為游戲結束時小華在第2個臺階，所以這包含兩種可能的情況：

第一種：小華在第1個臺階，并且小明在第2個臺階，最后一次劃拳小華平；

其概率為，

第二種：小華在第2個臺階，并且小明也在第2個臺階，最后一次劃拳小華輸，

其概率為

所以游戲結束時小華在第2個臺階的概率為．

（2）依題可知的可能取值為2、3、4、5，

，

，

，

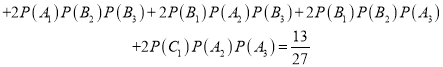
所以的分布列為：

	2	3	4	5

所以的數學期望為：

．