【答案】
分析:①檢驗f(x+
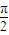
)=|sin(2x+π+
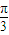
)-

|=|sin(2x+

π)
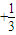
|≠f(x)可判斷①
②y=sin(x-
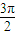
)=cosx在區在區間[π,

π]上單調遞增,可判斷②
③根據正弦函數與余弦函數在對稱軸處取得函數的最值,把x=
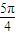
代入到函數y=sin(2x+

)=cos2x進行檢驗,可判斷③
④由x∈(0,π)可得0<sinx≤1,結合函數y=sinx+
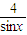
的單調性可判斷④
⑤、先設函數y=tan
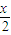
-cscx上任意一點M(x,y)關于點(π,0)對稱的點N(x′,y′),
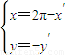
,代入到y=tan
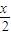
-cscx中可求對稱函數
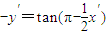
-csc(2π-x′),可判斷⑤
解答:解:∵f(x+
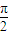
)=|sin(2x+π+
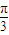
)-

|=|sin(2x+

π)
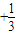
|≠f(x),而f(x+π)=|sin(2x+2π
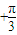
)-

|=|sin(2x+
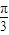
)
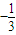
|=f(x),則函數的最小正周期是π,故①錯誤
②y=sin(x-
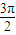
)=cosx在區在區間[π,

π]上單調遞增,故②錯誤
③x=
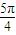
時,函數y=sin(2x+
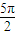
)=cos2x的值為0,不是最值點,不符合對稱軸的性質,故③錯誤
④∵x∈(0,π)
∴0<sinx≤1
y=sinx+
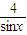
在sinx=1時取得最小值5
∴y的最小值不是4,故④錯誤
⑤設函數y=tan
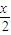
-cscx上任意一點M(x,y)關于點(π,0)對稱的點N(x′,y′)
則
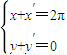
,即
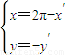
代入到y=tan
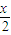
-cscx中可得
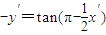
-csc(2π-x′)
∴
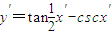
,即函數y=tan
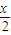
-cscx的圖象關于點(π,0)對稱,故⑤正確
故答案為:⑤
點評:本題主要考查了三角函數的周期的判斷,三角函數的誘導公式及函數的單調性的應用,函數的單調性在函數的最值求解中的應用及三角函數的對稱性的應用,屬于函數知識的綜合應用

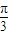 )-
)- |的最小正周期是
|的最小正周期是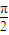 ;
;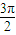 )在區間[π,
)在區間[π,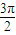 ]上單調遞減;
]上單調遞減;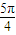 是函數y=sin(2x+
是函數y=sin(2x+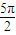 )的圖象的一條對稱軸;
)的圖象的一條對稱軸;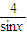 ,x∈(0,π)的最小值是4;
,x∈(0,π)的最小值是4;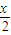 -cscx的一個對稱中心為點(π,0).
-cscx的一個對稱中心為點(π,0). 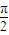 )=|sin(2x+π+
)=|sin(2x+π+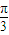 )-
)- |=|sin(2x+
|=|sin(2x+ π)
π)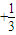 |≠f(x)可判斷①
|≠f(x)可判斷①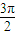 )=cosx在區在區間[π,
)=cosx在區在區間[π, π]上單調遞增,可判斷②
π]上單調遞增,可判斷②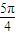 代入到函數y=sin(2x+
代入到函數y=sin(2x+ )=cos2x進行檢驗,可判斷③
)=cos2x進行檢驗,可判斷③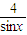 的單調性可判斷④
的單調性可判斷④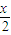 -cscx上任意一點M(x,y)關于點(π,0)對稱的點N(x′,y′),
-cscx上任意一點M(x,y)關于點(π,0)對稱的點N(x′,y′),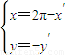 ,代入到y=tan
,代入到y=tan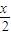 -cscx中可求對稱函數
-cscx中可求對稱函數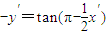 -csc(2π-x′),可判斷⑤
-csc(2π-x′),可判斷⑤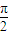 )=|sin(2x+π+
)=|sin(2x+π+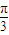 )-
)- |=|sin(2x+
|=|sin(2x+ π)
π)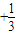 |≠f(x),而f(x+π)=|sin(2x+2π
|≠f(x),而f(x+π)=|sin(2x+2π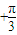 )-
)- |=|sin(2x+
|=|sin(2x+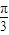 )
)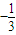 |=f(x),則函數的最小正周期是π,故①錯誤
|=f(x),則函數的最小正周期是π,故①錯誤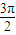 )=cosx在區在區間[π,
)=cosx在區在區間[π, π]上單調遞增,故②錯誤
π]上單調遞增,故②錯誤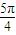 時,函數y=sin(2x+
時,函數y=sin(2x+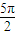 )=cos2x的值為0,不是最值點,不符合對稱軸的性質,故③錯誤
)=cos2x的值為0,不是最值點,不符合對稱軸的性質,故③錯誤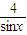 在sinx=1時取得最小值5
在sinx=1時取得最小值5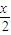 -cscx上任意一點M(x,y)關于點(π,0)對稱的點N(x′,y′)
-cscx上任意一點M(x,y)關于點(π,0)對稱的點N(x′,y′)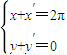 ,即
,即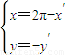
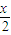 -cscx中可得
-cscx中可得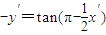 -csc(2π-x′)
-csc(2π-x′)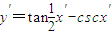 ,即函數y=tan
,即函數y=tan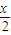 -cscx的圖象關于點(π,0)對稱,故⑤正確
-cscx的圖象關于點(π,0)對稱,故⑤正確

 .
. =1上一點,F1、F2分別為雙曲線的左右焦點,且|PF2|=4,則|PF1|=2或6.
=1上一點,F1、F2分別為雙曲線的左右焦點,且|PF2|=4,則|PF1|=2或6. .
. =1上一點,F1、F2分別為雙曲線的左右焦點,且|PF2|=4,則|PF1|=2或6.
=1上一點,F1、F2分別為雙曲線的左右焦點,且|PF2|=4,則|PF1|=2或6.