【答案】
分析:本題可用分析法來解答,分析法:證明使x
4+y
4≥
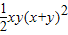
成立的充分條件成立,
解答:證明:要證x
4+y
4≥
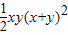
,只需證明2(x
4+y
4)≥xy(x+y)
2,
即證2(x
4+y
4)≥x
3y+xy
3+2x
2y
2,---------------------------(4分)
只需x
4+y
4≥x
3y+xy
3與x
4+y
4≥2x
2y
2同時成立即可,
又知x
4+y
4-2x
2y
2=(x
2-y
2)
2≥0,即x
4+y
4≥2x
2y
2成立,
只需再有x
4+y
4≥x
3y+xy
3成立即可,--------------------(8分)
由于x
4+y
4-x
3y-xy
3=(x-y)(x
3-y
3)
∵x-y與x
3-y
3同號,∴(x-y)(x
3-y
3)≥0,即x
4+y
4≥x
3y+xy
3成立,
∴對于任意實數x,y都有x
4+y
4≥

成立--------------(12分)
點評:本小題主要考查不等式的證明等基礎知識,考查運算變形能力,考查化歸與轉化思想.屬于基礎題.

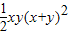 .
.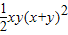 成立的充分條件成立,
成立的充分條件成立,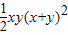 ,只需證明2(x4+y4)≥xy(x+y)2,
,只需證明2(x4+y4)≥xy(x+y)2, 成立--------------(12分)
成立--------------(12分)

 名校課堂系列答案
名校課堂系列答案