已知函數f(x)=x3+ax2+bx+c,在定義域x∈[-2,2]上表示的曲線過原點,且在x=±1處的切線斜率均為-1.有以下命題:
①f(x)是奇函數;②若f(x)在[s,t]內遞減,則|t-s|的最大值為4;③f(x)的最大值為M,最小值為m,則M+m=0; ④若對?x∈[-2,2],k≤f′(x)恒成立,則k的最大值為2.其中正確命題的序號為 .
【答案】
分析:由題意可得f(0)=0,f′(1)=f′(-1)=-1,代入可求a,b,c,進而可求f(x)
①由于f(-x)=-x
3+4x=-f(x),即f(x)是奇函數
②若f(x)在[s,t]內遞減,則t=
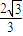
,s=-
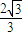
時|t-s|的最大;
③由奇函數的關于原點對稱可知,最大值與最小值互為相反數,
④若對?x∈[-2,2],由于f′(x)=3x
2-4∈[-4,8],則k≤f′(x)恒成立,則k≤f′(x)
min即可求解k,
解答:解:∵f(x)=x
3+ax
2+bx+c,在定義域x∈[-2,2]上表示的曲線過原點,
∴f(0)=0
∴c=0
∵f′(x)=3x
2+2ax+b,且在x=±1處的切線斜率均為-1.
∴f′(1)=f′(-1)=-1
∴
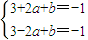
,解可得b=-4,a=0
∴f(x)=x
3-4x,f′(x)=3x
2-4
①∵f(-x)=-x
3+4x=-f(x),即f(x)是奇函數;①正確
②由f′(x)≥0得x
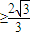
或x

f(x)在

內單調遞減,若f(x)在[s,t]內遞減,則,t=

,s=-
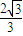
時|t-s|的最大值為
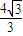
;②錯誤
③由奇函數的關于原點對稱可知,最大值與最小值互為相反數,f(x)的最大值為M,最小值為m,則M+m=0;③正確
④若對?x∈[-2,2],由于f′(x)=3x
2-4∈[-4,8],則k≤f′(x)恒成立,則k≤-4,則k的最大值為-4.④錯誤
正確命題的序號為①③
故答案為:①③
點評:本題主要考查了函數的導數的幾何意義的應用,函數的奇偶性及單調性等知識的綜合應用.

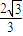 ,s=-
,s=-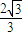 時|t-s|的最大;
時|t-s|的最大;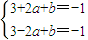 ,解可得b=-4,a=0
,解可得b=-4,a=0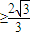 或x
或x f(x)在
f(x)在 內單調遞減,若f(x)在[s,t]內遞減,則,t=
內單調遞減,若f(x)在[s,t]內遞減,則,t= ,s=-
,s=-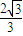 時|t-s|的最大值為
時|t-s|的最大值為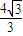 ;②錯誤
;②錯誤

 挑戰100單元檢測試卷系列答案
挑戰100單元檢測試卷系列答案 已知函數f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函數f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<