
【題目】如圖,設(shè)點![]() ,直線
,直線![]() ,點
,點![]() 在直線
在直線![]() 上移動,
上移動,![]() 是線段
是線段![]() 與
與![]() 軸的交點,
軸的交點,![]() ,
,![]() .
.

(1)求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)直線![]() 過點
過點![]() ,與軌跡
,與軌跡![]() 交于
交于![]() 兩點,過點
兩點,過點![]() 的直線與直線
的直線與直線![]() 交于點
交于點![]() ,求證:
,求證:![]() 軸.
軸.
【答案】(1)![]() (2)詳見解析
(2)詳見解析
【解析】
(1)先設(shè)![]() ,由題中條件得到
,由題中條件得到![]() ,根據(jù)
,根據(jù)![]() ,得到
,得到![]() ,進而可得出結(jié)果;
,進而可得出結(jié)果;
(2)先由題意設(shè)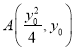 ,得到直線
,得到直線![]() 的方程為
的方程為![]() ,進而求出
,進而求出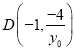 ;再由點
;再由點![]() 坐標,得到直線
坐標,得到直線![]() 的方程為
的方程為![]() ,聯(lián)立拋物線方程,結(jié)合韋達定理,求出
,聯(lián)立拋物線方程,結(jié)合韋達定理,求出![]() 點縱坐標,進而可證明結(jié)論成立.
點縱坐標,進而可證明結(jié)論成立.
(1)由題中條件,設(shè)![]() ,
,![]() ,
,
且![]() ,
,![]()
又![]() 與
與![]() 軸交于
軸交于![]() ,故
,故![]() ,
,
![]() ,
,![]()
![]() ,
,
故軌跡![]() 的方程為
的方程為![]() .
.
(2)設(shè)點![]() 為直線
為直線![]() 與軌跡
與軌跡![]() 的交點,由(1)設(shè)
的交點,由(1)設(shè)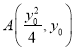 ,
,
則直線![]() 的方程為
的方程為![]() ,
,
故直線![]() 與
與![]() 的交點
的交點![]() 為
為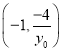 ,
,
又![]() ,
,![]() 直線
直線![]() 的方程為
的方程為 ,
,
即![]() ,
,
聯(lián)立拋物線![]() ,得:
,得:![]() ,
,
由韋達定理,![]() 兩點縱坐標乘積為
兩點縱坐標乘積為![]() ,
,
故![]() 點縱坐標為
點縱坐標為![]() ,與
,與![]() 點縱坐標相同,
點縱坐標相同,
又![]() ,
,![]() 軸.
軸.


科目:高中數(shù)學 來源: 題型:
【題目】甲、乙、丙、丁、戊五位媽媽相約各帶一個小孩去觀看花卉展,她們選擇共享電動車出行,每輛電動車只能載兩人,其中孩子們表示都不坐自己媽媽的車,甲的小孩一定要坐戊媽媽的車,則她們坐車不同的搭配方式有( )
A. ![]() 種 B.
種 B. ![]() 種 C.
種 C. ![]() 種 D.
種 D. ![]() 種
種
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知兩個正數(shù)a,b滿足a+b=1
(1)求證:![]() ;
;
(2)若不等式![]() 對任意正數(shù)a,b都成立,求實數(shù)x的取值范圍.
對任意正數(shù)a,b都成立,求實數(shù)x的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,AB是異面直線a、b的公垂線,長度為2,點C、D分別在直線a和b上,且CD長為4,過線段AB的中點M作平面α,使得AB⊥平面α,線段CD與平面α交點為N.


(1)求異面直線AB和CD所成的角的大小;
(2)求證:直線a∥α且CN=DN.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】過雙曲線C:![]() =1的右焦點F且與x軸不重合的直線交雙曲線C于A、B兩個點,定點D(
=1的右焦點F且與x軸不重合的直線交雙曲線C于A、B兩個點,定點D(![]() ,0).
,0).

(1)當直線AB垂直于x軸時,求直線AD的方程.
(2)設(shè)直線AD與直線x=1相交于點E,求證:FD∥BE.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓C:![]() ,直線l:y=kx+b與橢圓C相交于A、B兩點.
,直線l:y=kx+b與橢圓C相交于A、B兩點.
(1)如果k+b=﹣![]() ,求動直線l所過的定點;
,求動直線l所過的定點;
(2)記橢圓C的上頂點為D,如果∠ADB=![]() ,證明動直線l過定點P(0,﹣
,證明動直線l過定點P(0,﹣![]() );
);
(3)如果b=﹣![]() ,點B關(guān)于y軸的對稱點為B
,點B關(guān)于y軸的對稱點為B![]() ,向直線AB
,向直線AB![]() 是過定點?如果是,求出定點的坐標;如果不是,請說明理由.
是過定點?如果是,求出定點的坐標;如果不是,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知![]() ,
, ![]() ,
, ![]() .
.
(1)若![]() 是
是![]() 的充分不必要條件,求實數(shù)
的充分不必要條件,求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)若![]() ,“
,“![]() ”為真命題,“
”為真命題,“![]() ”為假命題,求實數(shù)
”為假命題,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知不等式組 表示的平面區(qū)域為
表示的平面區(qū)域為![]() ,若函數(shù)
,若函數(shù)![]() 的圖象上存在區(qū)域
的圖象上存在區(qū)域![]() 上的點,則實數(shù)
上的點,則實數(shù)![]() 的取值范圍是( )
的取值范圍是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com