
已知向量a=( ,
, ),b=(2,cos2x).
),b=(2,cos2x).
(1)若x∈(0, ],試判斷a與b能否平行?
],試判斷a與b能否平行?
(2)若x∈(0, ],求函數f(x)=a·b的最小值.
],求函數f(x)=a·b的最小值.
(1) a與b不能平行 (2) 2
【解析】本試題主要是考查而來向量的共線概念以及數量積的運算和三角函數性質的綜合運用。
(1)因為若a與b平行,則有 ·cos2x=
·cos2x=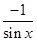 ·2,那么解方程可知方程無解。故a與b不能平行.
·2,那么解方程可知方程無解。故a與b不能平行.
(2)由于f(x)=a·b= -
-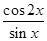 =
= =
=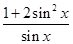 =2sinx+
=2sinx+ ,然后借助于均值不等式得到最值。
,然后借助于均值不等式得到最值。
解: (1)若a與b平行,則有 ·cos2x=
·cos2x=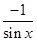 ·2,
……3分
·2,
……3分
因為x∈(0,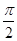 ],sinx≠0,所以得cos2x=-2,這與|cos2x|≤1相矛盾,
],sinx≠0,所以得cos2x=-2,這與|cos2x|≤1相矛盾,
故a與b不能平行. ……7分
(2)由于f(x)=a·b= -
-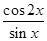 =
= =
=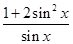 =2sinx+
=2sinx+ 10分
10分
又因為x∈(0,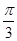 ],所以sinx∈(0,
],所以sinx∈(0,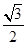 ],于是2sinx+
],于是2sinx+ ≥2
≥2 
=2  ,當2sinx=
,當2sinx= ,即sinx=
,即sinx=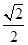 時取等號.
時取等號.
故函數f(x)的最小值等于2  . ……14分
. ……14分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
![]() 已知向量a=(cos
已知向量a=(cos![]() x,sin
x,sin![]() x),b=(cos
x),b=(cos![]() ,sin
,sin![]() ),c=(
),c=(![]() ,-1),其中x∈R,
,-1),其中x∈R,
(1)當a·b=![]() 時,求x值的集合;
時,求x值的集合;
(2)設函數f(x)=(a-c)2,求f(x)的最小正周期及![]() 其單調增區間.
其單調增區間.
查看答案和解析>>
科目:高中數學 來源:2012人教A版高中數學必修四2.5平面向量應用舉例練習題(解析版) 題型:選擇題
(2010·山東日照一中)已知向量a=(x1,y1),b=(x2,y2),若|a|=2,|b|=3,a·b=-6,則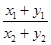 的值為( )
的值為( )
A. 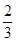 B.-
B.-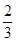
C. 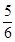 D.-
D.-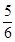
查看答案和解析>>
科目:高中數學 來源:2010-2011學年湖北省天門市高三天5月模擬文科數學試題 題型:選擇題
已知向量a=(1,2),a·b=5,| a-b |=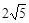 ,則| b |等于
,則| b |等于
A. B.
B.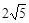 C.5 D.25
C.5 D.25
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com