
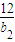 .
.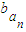 }是公比為9的等比數列,求證:
}是公比為9的等比數列,求證: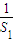 +
+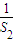 +…+
+…+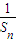 <
< .
. ,∴a1+a1+d=
,∴a1+a1+d= ,而a1=b1=1,則q(2+d)=12.①
,而a1=b1=1,則q(2+d)=12.① 或
或 (4分)
(4分) =b1
=b1 =q1+(n-1)d-1=q(n-1)d,
=q1+(n-1)d-1=q(n-1)d, =
= =qd=9,即qd=32.①(8分)
=qd=9,即qd=32.①(8分) .②
.② =n2.(10分)
=n2.(10分) =
= <
< =
= (
( -
- )(n≥2).
)(n≥2). +
+ ++
++ <1+
<1+ (
( -
- )+
)+ (
( -
- )+
)+ (
( -
- )++
)++ (
( -
-
 [(
[( -
- )+(
)+( -
- )+(
)+( -
- )+(
)+( -
- )]
)] (1+
(1+ -
- -
- )
) -
- -
- <
< .
. +
+ ++
++ <
< .(14分)
.(14分)

科目:高中數學 來源: 題型:
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| n1+n2+…+nm |
| m |
| r |
| m |
| an1+an2+…+anm |
| m |
| r |
| m |
| n1+n2+…+nm |
| m |
| r |
| m |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 | an |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com