
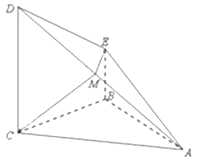
【題目】如圖,在四棱錐![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 為
為![]() 上一點,
上一點, ![]() 平面
平面![]() .
.
(Ⅰ)證明: ![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,求四棱錐
,求四棱錐![]() 的體積.
的體積.
【答案】(Ⅰ)詳見解析,(Ⅱ)2.
【解析】試題分析:(1)取線段![]() 的中點
的中點![]() ,連接
,連接![]() ,得出
,得出![]() ,再由
,再由![]() 平面
平面![]() ,證得
,證得![]() 平面
平面![]() ,進而利用線面平行的判定定理,即可證得
,進而利用線面平行的判定定理,即可證得![]() 平面
平面![]() ;
;
(2) 連接![]() ,得出
,得出![]() ,由(1)得出
,由(1)得出![]() ,因為
,因為![]() 是
是![]() 的中點,所以
的中點,所以![]() 是
是![]() 的中點,進而得出
的中點,進而得出![]() 平面
平面![]() ,利用棱錐的體積公式,即可求解幾何體的體積。
,利用棱錐的體積公式,即可求解幾何體的體積。
試題解析:
(Ⅰ)證明:取線段![]() 的中點
的中點![]() ,連接
,連接![]() .
.
因為![]() ,所以
,所以![]() ,
,
因為![]() 平面
平面![]() ,所以
,所以![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]() ,
,
因為![]() 平面
平面![]() ,所以
,所以![]() ,又
,又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)解:連接![]() ,因為
,因為![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
又平面![]() 平面
平面![]() ,所以
,所以![]() ,
,
由(Ⅰ)知![]() ,所以四邊形
,所以四邊形![]() 為平行四邊形,所以
為平行四邊形,所以![]() .
.
因為![]() 是
是![]() 的中點,所以
的中點,所以![]() 是
是![]() 的中點,
的中點,
所以![]() .
.
因為![]() 平面
平面![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以四棱錐![]() 的體積
的體積![]() .
.


 快樂暑假暑假能力自測中西書局系列答案
快樂暑假暑假能力自測中西書局系列答案科目:高中數學 來源: 題型:
【題目】空氣質量指數(![]() ,簡稱
,簡稱![]() )是定量描述空氣質量狀況的無量綱指數,參與空氣質量評價的主要污染物為
)是定量描述空氣質量狀況的無量綱指數,參與空氣質量評價的主要污染物為![]() 等六項.空氣質量按照
等六項.空氣質量按照![]() 大小分為六級:一級
大小分為六級:一級![]() 為優;二級
為優;二級![]() 為良好;三級
為良好;三級![]() 為輕度污染;四級
為輕度污染;四級![]() 為中度污染;五級
為中度污染;五級![]() 為重度污染;六級
為重度污染;六級![]() 為嚴重污染.
為嚴重污染.
某人根據環境監測總站公布的數據記錄了某地某月連續10天![]() 的莖葉圖如圖所示:
的莖葉圖如圖所示:

(1)利用訪樣本估計該地本月空氣質量優良(![]() )的天數;(按這個月總共30天計算);
)的天數;(按這個月總共30天計算);
(2)若從樣本中的空氣質量不佳(![]() )的這些天中,隨機地抽取三天深入分析各種污染指標,求這三天的空氣質量等級互不相同的概率.
)的這些天中,隨機地抽取三天深入分析各種污染指標,求這三天的空氣質量等級互不相同的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知長方形ABCD中,AB=3,AD=4.現將長方形沿對角線BD折起,使AC=a,得到一個四面體A-BCD,如圖所示.
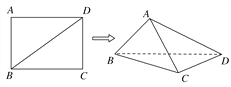
(1)試問:在折疊的過程中,直線AB與CD能否垂直?若能,求出相應a的值;若不能,請說明理由;
(2)求四面體A-BCD體積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐S-ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB.過A作AF⊥SB,垂足為F,點E,G分別是棱SA,SC的中點.

求證:(1)平面EFG∥平面ABC;
(2)BC⊥SA.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩袋中各裝有大小相同的小球9個,其中甲袋中紅色、黑色、白色小球的個數分別為2,3,4,乙袋中紅色、黑色、白色小球的個數均為3,某人用左右手分別從甲、乙兩袋中取球.
(1)若左右手各取一球,求兩只手中所取的球顏色不同的概率;
(2)若左右手依次各取兩球,稱同一手中兩球顏色相同的取法為成功取法,記兩次取球(左右手依次各取兩球為兩次取球)的成功取法次數為隨機變量X,求X的分布列。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,長方形物體E在雨中沿面P(面積為S)的垂直方向作勻速移動,速度為![]() ,雨速沿E移動方向的分速度為
,雨速沿E移動方向的分速度為![]() 。E移動時單位時間內的淋雨量包括兩部分:(1)P或P的平行面(只有一個面淋雨)的淋雨量,假設其值與
。E移動時單位時間內的淋雨量包括兩部分:(1)P或P的平行面(只有一個面淋雨)的淋雨量,假設其值與![]() ×S成正比,比例系數為
×S成正比,比例系數為![]() ;(2)其它面的淋雨量之和,其值為
;(2)其它面的淋雨量之和,其值為![]() ,記
,記![]() 為E移動過程中的總淋雨量,當移動距離d=100,面積S=
為E移動過程中的總淋雨量,當移動距離d=100,面積S=![]() 時。
時。
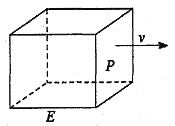
(1)寫出![]() 的表達式
的表達式
(2)設0<v≤10,0<c≤5,試根據c的不同取值范圍,確定移動速度![]() ,使總淋雨量
,使總淋雨量![]() 最少。
最少。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知橢圓![]() :
: ![]() 的左,右焦點分別為
的左,右焦點分別為![]() ,
, ![]() .點
.點![]() 是橢圓
是橢圓![]() 在
在![]() 軸上方的動點,且△
軸上方的動點,且△![]() 的周長為16.
的周長為16.
(1)求橢圓![]() 的方程;
的方程;
(2)設點![]() 到△
到△![]() 三邊的距離均相等.
三邊的距離均相等.
①當![]() 時,求點
時,求點![]() 的坐標;
的坐標;
②求證:點![]() 在定橢圓上.
在定橢圓上.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某醫療研究所開發一種新藥,如果成人按規定的劑量服用,據監測:服藥后每毫升血液中的含藥量y與時間t之間近似滿足如圖所示的曲線.

(1)寫出服藥后y與t之間的函數關系式;
(2)據測定,每毫升血液中含藥量不少于4 μg時治療疾病有效,假若某病人一天中第一次服藥為上午7:00,問:一天中怎樣安排服藥時間(共4次)效果最佳?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com