對于數列{an},從第二項起,每一項與它前一項的差依次組成等比數列,稱該等比數列為數列{an}的“差等比數列”,記為數列{bn}.設數列{bn}的首項b1=2,公比為q(q為常數).
(I)若q=2,寫出一個數列{an}的前4項;
(II)a1與q滿足什么條件,數列{an}是等比數列,并證明你的結論;
(III)若a1=1,數列{an+cn}是公差為q的等差數列,且c1=q,求數列{cn}的通項公式;并證明當1<q<2時,c5<-2q2.
解:(Ⅰ)因為數列{b
n}是等比數列,且b
1=2,q=2,所以b
2=4,b
3=8,
所以a
1=1,a
2=3,a
3=1,a
15=15.(寫出滿足條件的一組即可)…(2分)
(Ⅱ)因為數列{b
n}是等比數列,首項b
1=2,公比為q,,所以b
2=2q,b
3=2q
2,
所以a
2=a
1+2,a
3=a
1+2+2q.
因為數列{a
n}是等比數列,
所以
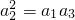
,即(a
1+2)
2=a
1×(a
1+2+2q)
所以
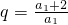
.
所以當
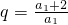
時,數列{a
n}是等比數列.…(5分)
(Ⅲ)因為{a
n+c
n}是公差為q的等差數列,所以(a
n+c
n)-(a
n-1+c
n-1)=q
∵a
n-a
n-1=2q
n-2,
∴c
n-c
n-1=q-2q
n-2,
∴c
n=c
1+(c
2-c
1)+…+(c
n-c
n-1)=nq-2(q
n-2+2q
n-3+…+q+1)=nq-
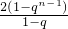
∴c
5=5q-
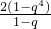
=-2q
3-2q
2+3q-2
∴c
5-(-2q
2)=2q(1-q
2)+(q-2).
∵1<q<2,∴1-q
2<0,q-2<0.
∴c
5-(-2q
2)<0
∴c
5<-2q
2. …(13分)
分析:(Ⅰ)根據數列{b
n}是等比數列,且b
1=2,q=2,可得b
2=4,b
3=8,由此可求個數列{a
n}的前4項;
(Ⅱ)先確定a
2=a
1+2,a
3=a
1+2+2q,根據數列{a
n}是等比數列,即可求出公比;
(Ⅲ)先確定c
n-c
n-1=q-2q
n-2,再利用疊加法,即可求數列{c
n}的通項公式,從而可證明1<q<2時,c
5<-2q
2.
點評:本題考查新定義,考查等比數列的證明,考查疊加法求數列的和,正確理解新定義是關鍵.

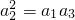 ,即(a1+2)2=a1×(a1+2+2q)
,即(a1+2)2=a1×(a1+2+2q)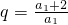 .
.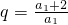 時,數列{an}是等比數列.…(5分)
時,數列{an}是等比數列.…(5分)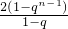
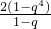 =-2q3-2q2+3q-2
=-2q3-2q2+3q-2
