
 +alnx,其中a≠0.
+alnx,其中a≠0. ,β=
,β= ,若|g(α)-g(β)|>|g(x1)-g(x2)|,求λ的取值范圍.
,若|g(α)-g(β)|>|g(x1)-g(x2)|,求λ的取值范圍.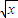 +alnx求導,驗證f′(1)≠0即可說明函數f(x)不具有“1-1駐點性”;②根據導數的符號和函數單調性的關系,即f′(x)>0時不等式解集就是函數的單調遞增區間,f′(x)<0時不等式解集就是函數的單調遞減區間,注意對參數a的討論;
+alnx求導,驗證f′(1)≠0即可說明函數f(x)不具有“1-1駐點性”;②根據導數的符號和函數單調性的關系,即f′(x)>0時不等式解集就是函數的單調遞增區間,f′(x)<0時不等式解集就是函數的單調遞減區間,注意對參數a的討論;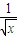 +
+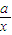
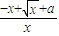 =
=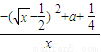
 <0,即a<-
<0,即a<- 時,f′(x)<0.∴f(x)是(0,+∞)上的減函數;
時,f′(x)<0.∴f(x)是(0,+∞)上的減函數; =0,即a=-
=0,即a=- 時,顯然f′(x)≤0.∴f(x)是(0,+∞)上的減函數
時,顯然f′(x)≤0.∴f(x)是(0,+∞)上的減函數 >0,即a>-
>0,即a>- 時,由f′(x)=0得
時,由f′(x)=0得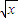 =
= ±
±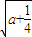
 <a<0時,
<a<0時, -
-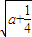 >0
>0 -
-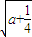 )時,f′(x)<0;
)時,f′(x)<0; -
-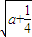 ,a+
,a+ +
+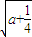 )時,f′(x)>0; x∈(a+
)時,f′(x)>0; x∈(a+ +
+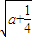 ,+∞)時,f′(x)<0;
,+∞)時,f′(x)<0; -
-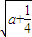 <0
<0 +
+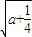 )時,f′(x)>0; x∈( a+
)時,f′(x)>0; x∈( a+ +
+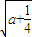 ,+∞)時,f′(x)<0;
,+∞)時,f′(x)<0; 時,函數f(x)的單調遞減區間為(0,+∞);
時,函數f(x)的單調遞減區間為(0,+∞); <a<0時,函數f(x)的單調遞減區間為(0,a+
<a<0時,函數f(x)的單調遞減區間為(0,a+ -
-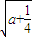 )和( a+
)和( a+ +
+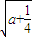 ,+∞),
,+∞), -
-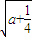 ,a+
,a+ +
+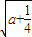 );
); +
+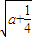 ),
), +
+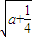 ,+∞)
,+∞)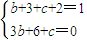 解得
解得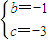
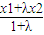 ≥
≥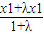 =x1,α=
=x1,α=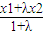 <
<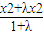 =x2,即α∈[x1,x2),同理β∈(x1,x2]
=x2,即α∈[x1,x2),同理β∈(x1,x2]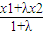 <
<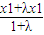 =x1,β=
=x1,β=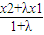 >
>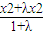 =x2
=x2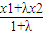 >
>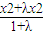 =x2,β=
=x2,β=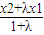 <
<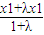 =x1,即β<x1<x2<α
=x1,即β<x1<x2<α

 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| x |
| x1+λx2 |
| 1+λ |
| x2+λx1 |
| 1+λ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 +alnx,其中a≠0.
+alnx,其中a≠0.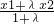 ,β=
,β=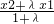 ,若|g(α)-g(β)|>|g(x1)-g(x2)|,求λ的取值范圍.
,若|g(α)-g(β)|>|g(x1)-g(x2)|,求λ的取值范圍.查看答案和解析>>
科目:高中數學 來源: 題型:
函數的導數為0的點稱為函數的駐點,若點(1,1)為函數f(x)的駐點,則稱f(x)具有“1—1駐點性”.
(1)設函數f(x)=-x+2![]() +alnx,其中a≠0。
+alnx,其中a≠0。
①求證:函數f(x)不具有“1—1駐點性”;②求函數f(x)的單調區間
(2)已知函數g(x)=bx3+3x2+cx+2具有“1—1駐點性”,給定x1,x2ÎR,x1<x2,設λ為實數,且λ≠-1,α=![]() ,β=
,β=![]() ,若|g(α)-g(β)|>|g(x1)-g(x2)|,求λ的取值范圍.
,若|g(α)-g(β)|>|g(x1)-g(x2)|,求λ的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com