
【題目】下列結(jié)論中不正確的個數(shù)是( )
①一個人打靶時連續(xù)射擊兩次,則事件“至少有一次中靶”與事件“至多有一次中靶”是對立事件;
②“![]() ”是“
”是“![]() ”的充分不必要條件;
”的充分不必要條件;
③若事件![]() 與事件
與事件![]() 滿足條件:
滿足條件:![]() ,則事件
,則事件![]() 與事件
與事件![]() 是對立事件;
是對立事件;
④把紅、橙、黃、綠4張紙牌隨機(jī)分給甲、乙、丙、丁4人,每人分得1張,則事件“甲分得紅牌”與事件“乙分得紅牌”是互斥事件.
A.1B.2C.3D.4
【答案】B
【解析】
根據(jù)對立事件定義可判斷①;由充分必要條件的判定可判斷②;根據(jù)對立事件的概率性質(zhì)可判斷③;根據(jù)互斥事件定義可判斷④.
對于①,因?yàn)閷α⑹录荒芡瑫r發(fā)生,但事件“至少有一次中靶”與事件“至多有一次中靶”都包含事件“射中一次靶”,所以不是對立事件,所以①錯誤;
對于②當(dāng)![]() 時,
時, ![]() ,所以“
,所以“![]() ”是“
”是“![]() ”的充分條件;當(dāng)
”的充分條件;當(dāng)![]() 時,
時,![]() 或
或![]()
![]() ,所以“
,所以“![]() ”不是“
”不是“![]() ”的必要條件,所以②正確;
”的必要條件,所以②正確;
對于③在同一試驗(yàn)條件下, 事件![]() 與事件
與事件![]() 滿足條件
滿足條件![]() 則事件
則事件![]() 與事件
與事件![]() 是對立事件;當(dāng)事件
是對立事件;當(dāng)事件![]() 與事件
與事件![]() 在不同的試驗(yàn)條件時,雖然滿足
在不同的試驗(yàn)條件時,雖然滿足![]() ,也不一定是對立事件,所以③錯誤;
,也不一定是對立事件,所以③錯誤;
對于④將4張紙牌隨機(jī)分給4人,事件“甲分得紅牌”與事件“乙分得紅牌”不能同時發(fā)生,也不是兩個中必有一個發(fā)生(即還有乙、丙可能得到紅牌),因而事件“甲分得紅牌”與事件“乙分得紅牌”是互斥事件,所以④正確
綜上可知,正確的為②④
故選:B



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,橢圓![]() 經(jīng)過點(diǎn)
經(jīng)過點(diǎn)![]() ,且點(diǎn)
,且點(diǎn)![]() 到橢圓的兩焦點(diǎn)的距離之和為
到橢圓的兩焦點(diǎn)的距離之和為![]() .
.
(l)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)若![]() 是橢圓
是橢圓![]() 上的兩個點(diǎn),線段
上的兩個點(diǎn),線段![]() 的中垂線
的中垂線![]() 的斜率為
的斜率為![]() 且直線
且直線![]() 與
與![]() 交于點(diǎn)
交于點(diǎn)![]() ,
,![]() 為坐標(biāo)原點(diǎn),求證:
為坐標(biāo)原點(diǎn),求證:![]() 三點(diǎn)共線.
三點(diǎn)共線.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,以原點(diǎn)為圓心,以橢圓的短半軸長為半徑的圓與直線
,以原點(diǎn)為圓心,以橢圓的短半軸長為半徑的圓與直線![]() 相切.
相切.

(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)過橢圓的右焦點(diǎn)![]() 的直線
的直線![]() 與橢圓交于A,B,過
與橢圓交于A,B,過![]() 與
與![]() 垂直的直線
垂直的直線![]() 與橢圓交于
與橢圓交于![]() ,
,![]() ,與
,與![]() 交于
交于![]() ,求證:直線
,求證:直線![]() ,
,![]() ,
,![]() 的斜率
的斜率![]() ,
,![]() ,
,![]() 成等差數(shù)列.
成等差數(shù)列.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某市為了了解民眾對開展創(chuàng)建文明城市工作以來的滿意度,隨機(jī)調(diào)查了40名群眾,并將他們隨機(jī)分成![]() ,
,![]() 兩組,每組20人,
兩組,每組20人,![]() 組群眾給第一階段的創(chuàng)文工作評分,
組群眾給第一階段的創(chuàng)文工作評分,![]() 組群眾給第二階段的創(chuàng)文工作評分,根據(jù)兩組群眾的評分繪制了如圖所示的莖葉圖.
組群眾給第二階段的創(chuàng)文工作評分,根據(jù)兩組群眾的評分繪制了如圖所示的莖葉圖.
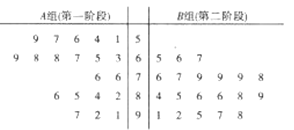
(Ⅰ)根據(jù)莖葉圖比較群眾對兩個階段的創(chuàng)文工作滿意度評分的平均值和集中程度(不要求計(jì)算出具體值,給出結(jié)論即可);
(Ⅱ)完成下面的列聯(lián)表,并通過計(jì)算判斷是否有![]() 的把握認(rèn)為民眾對兩個階段創(chuàng)文工作的滿意度存在差異?
的把握認(rèn)為民眾對兩個階段創(chuàng)文工作的滿意度存在差異?
低于70分 | 不低于70分 | 合計(jì) | |
第一階段 | |||
第二階段 | |||
合計(jì) |
參考公式:![]() ,
,![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知集合![]()
![]() .對于
.對于![]() ,定義
,定義![]() 與
與![]() 之間的距離為
之間的距離為![]() .
.
(Ⅰ)![]() ,寫出所有
,寫出所有![]() 的
的![]() ;
;
(Ⅱ)任取固定的元素![]() ,計(jì)算集合
,計(jì)算集合![]() 中元素個數(shù);
中元素個數(shù);
(Ⅲ)設(shè)![]() ,
,![]() 中有
中有![]() 個元素,記
個元素,記![]() 中所有不同元素間的距離的最小值為
中所有不同元素間的距離的最小值為![]() .證明:
.證明: ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】學(xué)校組織學(xué)生參加社會調(diào)查,某小組共有3名男同學(xué),4名女同學(xué),現(xiàn)從該小組中選出3名同學(xué)分別到甲乙丙三地進(jìn)行社會調(diào)查,若選出的同學(xué)中男女均有,則不同的安排方法有( )
A. 30種B. 60種C. 180種D. 360種
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓C:![]() 的離心率為
的離心率為![]() ,長半軸長為短軸長的b倍,A,B分別為橢圓C的上、下頂點(diǎn),點(diǎn)
,長半軸長為短軸長的b倍,A,B分別為橢圓C的上、下頂點(diǎn),點(diǎn)![]() .
.
![]() 求橢圓C的方程;
求橢圓C的方程;
![]() 若直線MA,MB與橢圓C的另一交點(diǎn)分別為P,Q,證明:直線PQ過定點(diǎn).
若直線MA,MB與橢圓C的另一交點(diǎn)分別為P,Q,證明:直線PQ過定點(diǎn).
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com