
【題目】如圖,在長方體ABCD﹣A′B′C′D′中,AB=2,AD=1,AA′=1.證明直線BC′平行于平面D′AC,并求直線BC′到平面D′AC的距離. 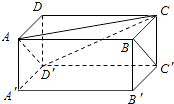
【答案】解:解法一:因為ABCD﹣A′B′C′D′為長方體,故AB∥C′D′,AB=C′D′,
故ABC′D′為平行四邊形,故BC′∥AD′,顯然BC′不在平面D′AC內,
于是直線BC′平行于平面D′AC.
直線BC′到平面D′AC的距離即為點B到平面D′AC的距離,設為h,
考慮三棱錐D′﹣ABC的體積,以ABC為底面,可得三棱錐D′﹣ABC的體積為V= ![]() (
( ![]() )=
)= ![]() ,
,
而△AD′C中,AC=D′C= ![]() ,AD′=
,AD′= ![]() ,故△CAD′的底邊AD′上的高為
,故△CAD′的底邊AD′上的高為 ![]() ,
,
故△CAD′的面積S△CAD′= ![]()
![]()
![]() =
= ![]() ,
,
所以,V= ![]() =
= ![]() h=
h= ![]() ,即直線BC′到平面D′AC的距離為
,即直線BC′到平面D′AC的距離為 ![]() .
.
解法二:以D′A′所在的直線為x軸,以D′C′所在的直線為y軸,以D′D所在的直線為z軸,
建立空間直角坐標系.
則由題意可得,點A(1,0,1 )、B(1,2,1)、C(0,2,1)、C′(0,2,0)、D′(0,0,0).
設平面D′AC的一個法向量為 ![]() =(u,v,w),則由
=(u,v,w),則由 ![]() ⊥
⊥ ![]() ,
, ![]() ⊥
⊥ ![]() ,可得
,可得 ![]() ,
, ![]() .
.
∵ ![]() =(1,0,1),
=(1,0,1), ![]() =(0,2,1),∴
=(0,2,1),∴ ![]() ,解得
,解得 ![]() .
.
令v=1,可得 u=2,w=﹣2,可得 ![]() =(2,1,﹣2).
=(2,1,﹣2).
由于 ![]() =(﹣1,0,﹣1),∴
=(﹣1,0,﹣1),∴ ![]() =﹣0,故有
=﹣0,故有 ![]() ⊥
⊥ ![]() .
.
再由BC′不在平面D′AC內,可得直線BC′平行于平面D′AC.
由于 ![]() =(1,0,0),可得點B到平面D′AC的距離d=
=(1,0,0),可得點B到平面D′AC的距離d= ![]() =
= 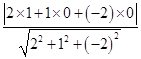 =
= ![]() ,
,
故直線BC′到平面D′AC的距離為 ![]() .
.
【解析】解法一:證明ABC′D′為平行四邊形,可得BC′∥AD′,再利用直線和平面平行的判定定理證得直線BC′平行于平面D′AC. 所求的距離即點B到平面D′AC的距離,設為h,再利用等體積法求得h的值.
解法二:建立空間直角坐標系,求出平面D′AC的一個法向量為 ![]() =(2,1,﹣2),再根據
=(2,1,﹣2),再根據 ![]() =﹣0,可得
=﹣0,可得 ![]() ⊥
⊥ ![]() ,可得直線BC′平行于平面D′AC.求出點B到平面D′AC的距離d=
,可得直線BC′平行于平面D′AC.求出點B到平面D′AC的距離d= ![]() 的值,即為直線BC′到平面D′AC的距離.
的值,即為直線BC′到平面D′AC的距離.
【考點精析】關于本題考查的直線與平面平行的判定,需要了解平面外一條直線與此平面內的一條直線平行,則該直線與此平面平行;簡記為:線線平行,則線面平行才能得出正確答案.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖,四棱柱ABCD﹣A1B1C1D1中,側棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E為棱AA1的中點. 
(1)證明B1C1⊥CE;
(2)求二面角B1﹣CE﹣C1的正弦值.
(3)設點M在線段C1E上,且直線AM與平面ADD1A1所成角的正弦值為 ![]() ,求線段AM的長.
,求線段AM的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】建設生態文明,是關系人民福祉,關乎民族未來的長遠大計.某市通宵營業的大型商場,為響應節能減排的號召,在氣溫超過![]() 時,才開放中央空調降溫,否則關閉中央空調.如圖是該市夏季一天的氣溫(單位:
時,才開放中央空調降溫,否則關閉中央空調.如圖是該市夏季一天的氣溫(單位:![]() )隨時間(
)隨時間(![]() ,單位:小時)的大致變化曲線,若該曲線近似的滿足函數
,單位:小時)的大致變化曲線,若該曲線近似的滿足函數![]() 關系.
關系.
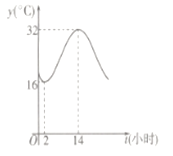
(1)求函數![]() 的表達式;
的表達式;
(2)請根據(1)的結論,判斷該商場的中央空調應在本天內何時開啟?何時關閉?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓![]() ,點B是其下頂點,過點B的直線交橢圓C于另一點A(A點在
,點B是其下頂點,過點B的直線交橢圓C于另一點A(A點在![]() 軸下方),且線段AB的中點E在直線
軸下方),且線段AB的中點E在直線![]() 上.
上.

(1)求直線AB的方程;
(2)若點P為橢圓C上異于A、B的動點,且直線AP,BP分別交直線![]() 于點M、N,證明:OM·ON為定值.
于點M、N,證明:OM·ON為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】分形幾何學是一門以不規則幾何形態為研究對象的幾何學.分形的外表結構極為復雜,但其內部卻是有規律可尋的.一個數學意義上分形的生成是基于一個不斷迭代的方程式,即一種基于遞歸的反饋系統.下面我們用分形的方法來得到一系列圖形,如圖1,線段![]() 的長度為a,在線段
的長度為a,在線段![]() 上取兩個點
上取兩個點![]() ,
,![]() ,使得
,使得![]() ,以
,以![]() 為一邊在線段
為一邊在線段![]() 的上方做一個正六邊形,然后去掉線段
的上方做一個正六邊形,然后去掉線段![]() ,得到圖2中的圖形;對圖2中的最上方的線段
,得到圖2中的圖形;對圖2中的最上方的線段![]() 作相同的操作,得到圖3中的圖形;依此類推,我們就得到了以下一系列圖形:
作相同的操作,得到圖3中的圖形;依此類推,我們就得到了以下一系列圖形:

記第![]() 個圖形(圖1為第1個圖形)中的所有線段長的和為
個圖形(圖1為第1個圖形)中的所有線段長的和為![]() ,現給出有關數列
,現給出有關數列![]() 的四個命題:
的四個命題:
①數列![]() 是等比數列;
是等比數列;
②數列![]() 是遞增數列;
是遞增數列;
③存在最小的正數![]() ,使得對任意的正整數
,使得對任意的正整數![]() ,都有
,都有![]() ;
;
④存在最大的正數![]() ,使得對任意的正整數
,使得對任意的正整數![]() ,都有
,都有![]() .
.
其中真命題的序號是________________(請寫出所有真命題的序號).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】環保組織隨機抽檢市內某河流2015年內100天的水質,檢測單位體積河水中重金屬含量![]() ,并根據抽檢數據繪制了如下圖所示的頻率分布直方圖.
,并根據抽檢數據繪制了如下圖所示的頻率分布直方圖.
(Ⅰ)求圖中![]() 的值;
的值;
(Ⅱ)假設某企業每天由重金屬污染造成的經濟損失![]() (單位:元)與單位體積河水中重金屬含量
(單位:元)與單位體積河水中重金屬含量![]()
的關系式為 ,若將頻率視為概率,在本年內隨機抽取一天,試估計這天經濟損失不超過500元的概率.
,若將頻率視為概率,在本年內隨機抽取一天,試估計這天經濟損失不超過500元的概率.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C的兩個焦點分別為F1(﹣1,0)、F2(1,0),短軸的兩個端點分別為B1 , B2
(1)若△F1B1B2為等邊三角形,求橢圓C的方程;
(2)若橢圓C的短軸長為2,過點F2的直線l與橢圓C相交于P,Q兩點,且 ![]() ,求直線l的方程.
,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() .
.
(1)若直線![]() 不經過第四象限,求
不經過第四象限,求![]() 的取值范圍;
的取值范圍;
(2)若直線![]() 交
交![]() 軸負半軸于點
軸負半軸于點![]() ,交
,交![]() 軸正半軸于點
軸正半軸于點![]() ,
,![]() 為坐標原點,設
為坐標原點,設![]() 的面積為
的面積為![]() ,求
,求![]() 的最小值及此時直線
的最小值及此時直線![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com