
一個袋子里裝有7個球,其中有紅球4個, 編號分別為1,2,3,4;白球3個,編號分別為1,2,3.從袋子中任取4個球(假設取到任何一個球的可能性相同).
(Ⅰ)求取出的4個球中, 含有編號為3的球的概率;
(Ⅱ)在取出的4個球中, 紅球編號的最大值設為X,求隨機變量X的分布列和數學期望.
(Ⅰ)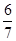 ;(Ⅱ)
;(Ⅱ)
|
X |
1 |
2 |
3 |
4 |
|
P |
|
|
|
|
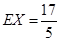 .
.
【解析】
試題分析:(Ⅰ)分別算出取出四個球的取法數以及取出的4個球中含有編號為3的球的取法種數,后者與前者之比即為所求.(Ⅱ)可知隨機變量X的所有可能取值為1,2,3,4.然后將每種可能取值的概率計算出,即可列出分布表.再由期望的計算公式即可得出期望.
試題解析:(Ⅰ)設“取出的4個球中,含有編號為3的球”為事件A,
由題意,取出四個球共有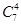 取法.其中含有編號為3的球的取法有
取法.其中含有編號為3的球的取法有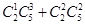 種.
種.
則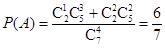 .
.
所以,取出的4個球中,含有編號為3的球的概率為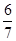 .
4分
.
4分
(Ⅱ)隨機變量X的所有可能取值為1,2,3,4.
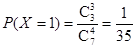 ,
, 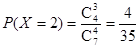 ,
,
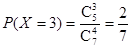 ,
, 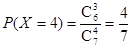 ,
8分
,
8分
所以隨機變量X的分布列是
|
X |
1 |
2 |
3 |
4 |
|
P |
|
|
|
|
隨機變量X的數學期望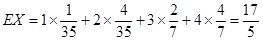 . 12分
. 12分
考點:1.隨機事件的概率;2.離散型隨機變量及分布列;3.期望.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源:2014屆浙江省溫州八校高三9月期初聯考理科數學試卷(解析版) 題型:解答題
一個袋子里裝有7個球, 其中有紅球4個, 編號分別為1,2,3,4; 白球3個, 編號分別為2,3,4. 從袋子中任取4個球 (假設取到任何一個球的可能性相同).
(Ⅰ) 求取出的4個球中, 含有編號為3的球的概率;
(Ⅱ) 在取出的4個球中, 紅球編號的最大值設為X ,求隨機變量X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數學 來源:2013-2014學年浙江省溫州市八校聯考高三(上)9月月考數學試卷(理科)(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com