
【題目】網上購物逐步走進大學生活,某大學學生宿舍4人積極參加網購,大家約定:每個人通過擲一枚質地均勻的骰子決定自己去哪家購物,擲出點數為5或6的人去淘寶網購物,擲出點數小于5的人去京東商城購物,且參加者必須從淘寶網和京東商城選擇一家購物.
(1)求這4個人中恰有1人去淘寶網購物的概率;
(2)用![]() ,
,![]() 分別表示這4個人中去淘寶網和京東商城購物的人數,記
分別表示這4個人中去淘寶網和京東商城購物的人數,記![]() ,求隨機變量
,求隨機變量![]() 的分布列與數學期望
的分布列與數學期望![]() .
.
【答案】(1)![]() ;(2)分布列詳見解析,
;(2)分布列詳見解析,![]() .
.
【解析】
試題本題主要考查概率、離散型隨機變量的分布列和數學期望等基礎知識,考查學生的分析問題解決問題的能力、轉化能力、計算能力.第一問,先求出每個人去淘寶網購物的概率![]() ,去京東商城購物的概率
,去京東商城購物的概率![]() ,再利用二項分布計算恰有1人去淘寶購物的概率;第二問,先寫出X的所有可能取值,再利用二項分布分布求出概率,列出分布列,再利用
,再利用二項分布計算恰有1人去淘寶購物的概率;第二問,先寫出X的所有可能取值,再利用二項分布分布求出概率,列出分布列,再利用![]() 求出隨機變量X的數學期望.
求出隨機變量X的數學期望.
試題解析:依題意,這4個人中,每個人去淘寶網購物的概率為![]() ,去京東商城購物的概率為
,去京東商城購物的概率為![]() .設“這4個人中恰有i人去淘寶網購物”為事件
.設“這4個人中恰有i人去淘寶網購物”為事件![]() ,則
,則![]() .
.
(Ⅰ)這4個人中恰有1人去淘寶網購物的概率![]() .
.
(II)易知![]() 的所有可能取值為
的所有可能取值為![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
所以![]() 的分布列是
的分布列是
| 0 | 3 | 4 |
P |
|
|
|
隨機變量ξ的數學期望![]() .
.


科目:高中數學 來源: 題型:
【題目】小明跟父母、爺爺奶奶一同參加《中國詩詞大會》的現場錄制,5人坐成一排.若小明的父母至少有一人與他相鄰,則不同坐法的總數為
A. 60 B. 72 C. 84 D. 96
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 過點
過點![]() ,直線
,直線![]() 過點
過點![]() 與拋物線
與拋物線![]() 交于
交于![]() ,
, ![]() 兩點.點
兩點.點![]() 關于
關于![]() 軸的對稱點為
軸的對稱點為![]() ,連接
,連接![]() .
.

(1)求拋物線線![]() 的標準方程;
的標準方程;
(2)問直線![]() 是否過定點?若是,求出定點坐標;若不是,請說明理由.
是否過定點?若是,求出定點坐標;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了貫徹落實中央省市關于新型冠狀病毒肺炎疫情防控工作要求,積極應對新型冠狀病毒疫情,切實做好2020年春季開學工作,保障校園安全穩定,普及防控知識,確保師生生命安全和身體健康.某校開學前,組織高三年級800名學生參加了“疫情防控”網絡知識競賽(滿分150分).已知這800名學生的成績均不低于90分,將這800名學生的成績分組如下:第一組![]() ,第二組
,第二組![]() ,第三組
,第三組![]() ,第四組
,第四組![]() ,第五組
,第五組![]() ,第六組
,第六組![]() ,得到的頻率分布直方圖如圖所示.
,得到的頻率分布直方圖如圖所示.

(1)求![]() 的值并估計這800名學生的平均成績(同一組中的數據用該組區間的中點值代表);
的值并估計這800名學生的平均成績(同一組中的數據用該組區間的中點值代表);
(2)該校“群防群控”督查組為更好地督促高三學生的“個人防控”,準備從這800名學生中取2名學生參與督查工作,其取辦法是:先在第二組第五組第六組中用分層抽樣的方法抽取6名學生,再從這6名學生中隨機抽取2名學生.記這2名學生的競賽成績分別為![]()
![]() .求事件
.求事件![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在數列![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,其中
,其中![]() .
.
⑴ 求證:數列![]() 為等差數列;
為等差數列;
⑵ 設![]() ,
, ![]() ,數列
,數列![]() 的前
的前![]() 項和為
項和為![]() ,若當
,若當![]() 且
且![]() 為偶數時,
為偶數時, ![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
⑶ 設數列![]() 的前
的前![]() 項的和為
項的和為![]() ,試求數列
,試求數列![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2017安徽蚌埠一模)已知橢圓C:![]() =1(a>b>0)的離心率為
=1(a>b>0)的離心率為![]() ,F1,F2是橢圓的兩個焦點,P是橢圓上任意一點,且△PF1F2的周長是8+2
,F1,F2是橢圓的兩個焦點,P是橢圓上任意一點,且△PF1F2的周長是8+2![]() .
.

(1)求橢圓C的方程;
(2)設圓T:(x-2)2+y2=![]() ,過橢圓的上頂點M作圓T的兩條切線交橢圓于E,F兩點,求直線EF的斜率.
,過橢圓的上頂點M作圓T的兩條切線交橢圓于E,F兩點,求直線EF的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐PABC中,不能證明AP⊥BC的條件是( )
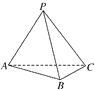
A. AP⊥PB,AP⊥PC
B. AP⊥PB,BC⊥PB
C. 平面BPC⊥平面APC,BC⊥PC
D. AP⊥平面PBC
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com