
【題目】已知函數![]()
(Ⅰ)若直線![]() 且曲線
且曲線![]() 在A處的切線與
在A處的切線與![]() 在B處的切線相互平行,求a的取值范圍;
在B處的切線相互平行,求a的取值范圍;
(Ⅱ)設![]() 在其定義域內有兩個不同的極值點
在其定義域內有兩個不同的極值點![]() 且
且![]() 若不等式
若不等式![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() .
.
【解析】試題分析:(Ⅰ)求出![]() 可得
可得![]() 在
在![]() 有解,轉化為函數
有解,轉化為函數![]() 與
與![]() 的圖象在
的圖象在![]() 上有交點,求出相切時
上有交點,求出相切時![]() ,利用數形結合思想可得結果;(Ⅱ)根據極值點的定義可得
,利用數形結合思想可得結果;(Ⅱ)根據極值點的定義可得![]() ,作差可得
,作差可得![]() ,
, ![]() 等價于
等價于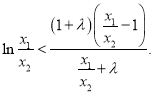 令
令![]() ,則
,則![]() ,不等式
,不等式![]() 在
在![]() 上恒成立,討論兩種情況,分別利用導數研究函數的單調性,根據單調性可得函數最值,從而篩選符合題意的
上恒成立,討論兩種情況,分別利用導數研究函數的單調性,根據單調性可得函數最值,從而篩選符合題意的![]() 的取值范圍.
的取值范圍.
試題解析:(Ⅰ)依題意,函數![]() 的定義域為(0,
的定義域為(0, ![]() ),
),![]() 因為曲線
因為曲線![]() 在A處的切線與
在A處的切線與![]() 在B處的切線相互平行,所以
在B處的切線相互平行,所以![]() 有解,即方程
有解,即方程![]() 有解.
有解.
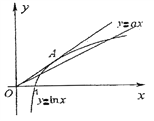
方程![]() 有解轉化為函數
有解轉化為函數![]() 的圖像在
的圖像在![]() 上有交點,
上有交點,
如圖,令過原點且與函數![]() 的圖像相切的直線的斜率為
的圖像相切的直線的斜率為![]() ,只須
,只須![]()
令切點為![]() ,所以
,所以![]()
![]() ,所以
,所以![]()
(Ⅱ)![]()
因為![]() 在其定義域內有兩個不同的極值點,所以
在其定義域內有兩個不同的極值點,所以![]() 的兩個根,即
的兩個根,即![]()
因為![]()
![]()
![]()
![]()
![]()
![]()
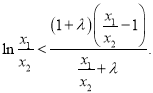
令![]() ,則
,則![]() ,由題意知,不等式
,由題意知,不等式![]() 上恒成立.
上恒成立.
令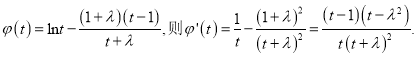
如果![]() 所以
所以![]() 上單調遞增,又
上單調遞增,又![]()
![]()
![]() 上恒成立,符合題意.
上恒成立,符合題意.
如果![]() 時,
時, ![]()
![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,又
上單調遞減,又![]() 上不能恒小于0,不符合題意,舍去.
上不能恒小于0,不符合題意,舍去.
綜上所述,若不等式![]() 恒成立,只須
恒成立,只須![]() .
.


 導學教程高中新課標系列答案
導學教程高中新課標系列答案 小學課時特訓系列答案
小學課時特訓系列答案科目:高中數學 來源: 題型:
【題目】隨著資本市場的強勢進入,互聯網共享單車“忽如一夜春風來”,遍布了一二線城市的大街小巷.為了解共享單車在![]() 市的使用情況,某調查機構借助網絡進行了問卷調查,并從參與調查的網友中隨機抽取了200人進行抽樣分析,得到下表(單位:人):
市的使用情況,某調查機構借助網絡進行了問卷調查,并從參與調查的網友中隨機抽取了200人進行抽樣分析,得到下表(單位:人):
經常使用 | 偶爾或不用 | 合計 | |
30歲及以下 | 70 | 30 | 100 |
30歲以上 | 60 | 40 | 100 |
合計 | 130 | 70 | 200 |
(1)根據以上數據,能否在犯錯誤的概率不超過0.15的前提下認為![]() 市使用共享單車情況與年齡有關?
市使用共享單車情況與年齡有關?
(2)現從所有抽取的30歲以上的網民中利用分層抽樣抽取5人,
![]() 求這5人中經常使用、偶爾或不用共享單車的人數;
求這5人中經常使用、偶爾或不用共享單車的人數;
![]() 從這5人中,在隨機選出2人贈送一件禮品,求選出的2人中至少有1人經常使用共享單車的概率.
從這5人中,在隨機選出2人贈送一件禮品,求選出的2人中至少有1人經常使用共享單車的概率.
參考公式: 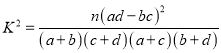 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列命題,其中正確的序號是________(寫出所有正確命題的序號).
①已知集合![]() ,
,![]() ,則映射
,則映射![]() 中滿足
中滿足![]() 的映射共有
的映射共有![]() 個;
個;
②函數![]() 的圖象關于
的圖象關于![]() 對稱的函數解析式為
對稱的函數解析式為![]() ;
;
③若函數![]() 的值域為
的值域為![]() ,則實數
,則實數![]() 的取值范圍是
的取值范圍是![]() ;
;
④已知函數![]() 的最大值為
的最大值為![]() ,最小值為
,最小值為![]() ,則
,則![]() 的值等于
的值等于![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,一個圓錐的底面半徑為1,高為3,在圓錐中有一個半徑為x的內接圓柱.

(1)試用x表示圓柱的高;
(2)當x為何值時,圓柱的側面積最大,最大側面積是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2-2ax-1+a,a∈R.
(1)若a=2,試求函數y=![]() (x>0)的最小值;
(x>0)的最小值;
(2)對于任意的x∈[0,2],不等式f(x)≤a成立,試求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為正方形,且
為正方形,且![]() ,其中
,其中![]() ,
,![]() ,
,![]() 分別是
分別是![]() ,
,![]() ,
,![]() 的中點,動點
的中點,動點![]() 在線段
在線段![]() 上運動時,下列四個結論:①
上運動時,下列四個結論:①![]() ;②
;②![]() ;③
;③![]() 面
面![]() ;④
;④![]() 面
面![]() ,
,
其中恒成立的為( )

A. ①③ B. ③④ C. ①④ D. ②③
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校做了一次關于“感恩父母”的問卷調查,從8~10歲,11~12歲,13~14歲,15~16歲四個年齡段回收的問卷依次為:120份,180份,240份,x份.因調查需要,從回收的問卷中按年齡段分層抽取容量為300的樣本,其中在11~12歲學生問卷中抽取60份,則在15~16歲學生中抽取的問卷份數為( )
A.60 B.80 C.120 D.180
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x|x-a|+bx.
(1)若a=2,且f(x)是R上的增函數,求實數b的取值范圍;
(2)當b=0時,若關于x的方程f(x)=x+1有三個實根,求a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com