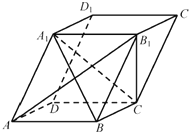
【題目】在平行六面體
中，
．
求證：（1）
；
（2）
．
【答案】答案見解析
【解析】分析：（1）先根據平行六面體得線線平行，再根據線面平行判定定理得結論；（2）先根據條件得菱形ABB1A1，再根據菱形對角線相互垂直，以及已知垂直條件，利用線面垂直判定定理得線面垂直，最后根據面面垂直判定定理得結論.
詳解：
證明：（1）在平行六面體ABCD-A1B1C1D1中，AB∥A1B1．
因為AB
平面A1B1C，A1B1
平面A1B1C，
所以AB∥平面A1B1C．
（2）在平行六面體ABCD-A1B1C1D1中，四邊形ABB1A1為平行四邊形．
又因為AA1=AB，所以四邊形ABB1A1為菱形，
因此AB1⊥A1B．
又因為AB1⊥B1C1，BC∥B1C1，
所以AB1⊥BC．
又因為A1B∩BC=B，A1B平面A1BC，BC平面A1BC，
所以AB1⊥平面A1BC．
因為AB1平面ABB1A1，
所以平面ABB1A1⊥平面A1BC．
科目：高中數學 來源： 題型：
【題目】某地空氣中出現污染，須噴灑一定量的去污劑進行處理.據測算，每噴灑1個單位的去污劑，空氣中釋放的濃度y（單位：毫克/立方米）隨著時間x（單位：天）變化的函數關系式近似為
，若多次噴灑，則某一時刻空氣中的去污劑濃度為每次投放的去污劑在相應時刻所釋放的濃度之和.由實驗知，當空氣中去污劑的濃度不低于4（毫克/立方米）時，它才能起到去污作用.
（Ⅰ）若一次噴灑4個單位的去污劑，則去污時間可達幾天？
（Ⅱ）若第一次噴灑2個單位的去污劑，6天后再噴灑
個單位的去污劑，要使接下來的4天中能夠持續有效去污，試求的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，圓C的參數方程為 
（θ為參數），以O為極點，x軸的非負半軸為極軸且取相同的單位長度建立極坐標系．
（1）求圓C的極坐標方程；
（2）若直線l的極坐標方程是 
，射線 
與圓C的交點為O、P，與直線l的交點為Q．求線段PQ的長．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，圓C的參數方程為 
（θ為參數），以O為極點，x軸的非負半軸為極軸且取相同的單位長度建立極坐標系．
（1）求圓C的極坐標方程；
（2）若直線l的極坐標方程是 
，射線 
與圓C的交點為O、P，與直線l的交點為Q．求線段PQ的長．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某項“過關游戲”規則規定：在地
關要拋擲
顆骰子次，如果這次拋擲所出現的點數和大于
，則算過關．
（Ⅰ）此游戲最多能過__________關．
（Ⅱ）連續通過第關、第
關的概率是__________．
（Ⅲ）若直接挑戰第
關，則通關的概率是__________．
（Ⅳ）若直接挑戰第
關，則通關的概率是__________．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數 
（ 
），若函數F（x）=f（x）﹣3的所有零點依次記為x1 ， x2 ， x3 ， …，xn ， 且x1＜x2＜x3＜…＜xn ， 則x1+2x2+2x3+…+2xn﹣1+xn= ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，甲、乙兩個企業的用電負荷量
關于投產持續時間
（單位：小時）的關系
均近似地滿足函數
．
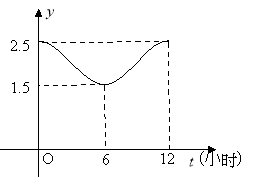
（1）根據圖象，求函數
的解析式；
（2）為使任意時刻兩企業用電負荷量之和不超過
，現采用錯峰用電的方式，讓企業乙比企業甲推遲
小時投產，求的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知命題
函數
是
上的奇函數，命題
函數
的定義域和值域都是
，其中
.
（1）若命題
為真命題，求實數
的值；
（2）若“且
”為假命題，“或”為真命題，求實數的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
