
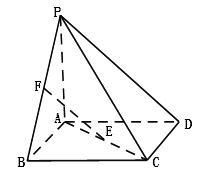
【題目】如圖,四棱錐 ![]() 的底面
的底面 ![]() 為正方形,
為正方形, ![]() ⊥底面
⊥底面 ![]() ,
, ![]() 分別是
分別是 ![]() 的中點,
的中點, ![]() .
.
(Ⅰ)求證 ![]() ∥平面
∥平面 ![]() ;
;
(Ⅱ)求直線 ![]() 與平面
與平面 ![]() 所成的角;
所成的角;
(Ⅲ)求四棱錐 ![]() 的外接球的體積.
的外接球的體積.
【答案】解:(Ⅰ)如圖,連結 ![]() ,則
,則 ![]() 是
是 ![]() 的中點,又
的中點,又 ![]() 是
是 ![]() 的中點,
的中點,
∴ ![]() .又∵
.又∵ ![]() 平面
平面 ![]() ,
, ![]() 面
面 ![]()
∴ ![]() 平面
平面 ![]() .
.
(Ⅱ)取 ![]() 的中點
的中點 ![]() ,連接
,連接 ![]() .
.
在正方形 ![]() 中,
中, ![]() 是
是 ![]() 的中點,有
的中點,有 ![]() .
.
∵ ![]() 平面
平面 ![]() ,
, ![]() 平面
平面 ![]() ,∴
,∴ ![]() ,
,
∵ ![]() ,∴
,∴ ![]() 平面
平面 ![]() ,
,
∴ ![]() 是直線
是直線 ![]() 在平面
在平面 ![]() 的射影,∴
的射影,∴ ![]() 是直線
是直線 ![]() 與平面
與平面 ![]() 所成的角,
所成的角,
在直角三角形 ![]() 中,
中, ![]() ,所以
,所以 ![]() .
.
∴直線 ![]() 與平面
與平面 ![]() 所成的角為45°.
所成的角為45°.
(Ⅲ)設四棱錐 ![]() 的外接球半徑為
的外接球半徑為 ![]() ,
, ![]() ,則
,則
![]() ,即
,即 ![]() .
.
所以外接球的體積為 ![]() ..
..
【解析】(1)根據題意作出輔助線,利用線面平行的判定定理即可得證。(2)由題意結合線面垂直的判斷定理可得證H E ⊥ 平面 P A B,進而找出二面角的平面角結合題中已知在直角三角形中求出線面角即可。(3)根據題意把四棱錐補成為一個球內接長方體,球的直徑為長方體的體對角線進而求出半徑再結合球的體積公式代入數值求出即可。
【考點精析】本題主要考查了直線與平面平行的性質和直線與平面垂直的判定的相關知識點,需要掌握一條直線與一個平面平行,則過這條直線的任一平面與此平面的交線與該直線平行;簡記為:線面平行則線線平行;一條直線與一個平面內的兩條相交直線都垂直,則該直線與此平面垂直;注意點:a)定理中的“兩條相交直線”這一條件不可忽視;b)定理體現了“直線與平面垂直”與“直線與直線垂直”互相轉化的數學思想才能正確解答此題.


 中考解讀考點精練系列答案
中考解讀考點精練系列答案 各地期末復習特訓卷系列答案
各地期末復習特訓卷系列答案科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C的對邊分別為a,b,c,若a2+c2+ ![]() ac=b2 , sinA=
ac=b2 , sinA= ![]() .
.
(1)求sinC的值;
(2)若a=2,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設區間D=[﹣3,3],定義在D上的函數f(x)=ax3+bx+1(a>0,b∈R),集合A={a|x∈D,f(x)≥0}.
(1)若b= ![]() ,求集合A;
,求集合A;
(2)設常數b<0 ①討論f(x)的單調性;
②若b<﹣1,求證:A=.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某淘寶商城在2017年前7個月的銷售額![]() (單位:萬元)的數據如下表,已知
(單位:萬元)的數據如下表,已知![]() 與
與![]() 具有較好的線性關系.
具有較好的線性關系. 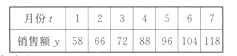
(1)求![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(2)分析該淘寶商城2017年前7個月的銷售額的變化情況,并預測該商城8月份的銷售額.
附:回歸直線的斜率和截距的最小二乘估計公式分別為:
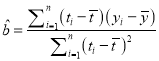 ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設 ![]() 是兩個平面,
是兩個平面, ![]() 是兩條直線,有下列四個命題:
是兩條直線,有下列四個命題:
⑴如果 ![]() ,那么
,那么 ![]() .
.
⑵如果 ![]() ,那么
,那么 ![]() .
.
⑶如果 ![]() ,那么
,那么 ![]() .
.
其中正確命題的個數是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設集合M={x||x|<1},N={y|y=2x , x∈M},則集合R(M∩N)等于( )
A.(﹣∞, ![]() ]
]
B.( ![]() ,1)
,1)
C.(﹣∞, ![]() ]∪[1,+∞)
]∪[1,+∞)
D.[1,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義在R上的奇函數f(x),當x≥0時,f(x)= ![]() ,則關于x的函數F(x)=f(x)﹣a(0<a<1)的所有零點之和為( )
,則關于x的函數F(x)=f(x)﹣a(0<a<1)的所有零點之和為( )
A.3a﹣1
B.1﹣3a
C.3﹣a﹣1
D.1﹣3﹣a
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 上的一個最高點的坐標為
上的一個最高點的坐標為![]() ,由此點到相鄰最低點間的曲線與x軸交于點
,由此點到相鄰最低點間的曲線與x軸交于點![]() ,若
,若![]() .
.
(1)求![]() 的解析式.
的解析式.
(2)求![]() 在
在![]() 上的值域.
上的值域.
(3)若對任意實數![]() ,不等式
,不等式![]() 在
在![]() 上恒成立,求實數
上恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com