
已知函數
 .
.
(1)若曲線 經過點
經過點 ,曲線
,曲線 在點
在點 處的切線與直線
處的切線與直線 垂直,求
垂直,求 的值;
的值;
(2)在(1)的條件下,試求函數 (
( 為實常數,
為實常數, )的極大值與極小值之差;
)的極大值與極小值之差;
(3)若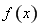 在區間
在區間 內存在兩個不同的極值點,求證:
內存在兩個不同的極值點,求證: .
.
(1)
(2)當 或
或 時,
時,
 ;
;
當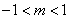 時,
時,
 ;
;
(3) .
.
【解析】
試題分析:(1)利用導數的幾何意義,明確曲線 在點
在點 處的切線的斜率為
處的切線的斜率為 ,建立方程
,建立方程
 ,再根據曲線
,再根據曲線 經過點
經過點 ,得到方程
,得到方程 ,解方程組即得所求.
,解方程組即得所求.
(2)利用“表解法”,確定函數的極值,注意討論 或
或 及
及 ,的不同情況;
,的不同情況;
(3)根據 在區間
在區間 內存在兩個極值點,得到
內存在兩個極值點,得到 ,
,
即 在
在 內有兩個不等的實根.
內有兩個不等的實根.
利用二次函數的圖象和性質建立不等式組 求
求 的范圍.
的范圍.
試題解析:(1)
 ,
,
 直線
直線 的斜率為
的斜率為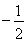 ,
, 曲線
曲線 在點
在點 處的切線的斜率為
處的切線的斜率為 ,
,
 ①
①
 曲線
曲線 經過點
經過點 ,
, ②
②
由①②得: 3分
3分
(2)由(1)知: ,
,
 ,
, , 由
, 由 ,或
,或 .
.
當 ,即
,即 或
或 時,
時, ,
, ,
, 變化如下表
變化如下表
|
|
|
|
|
|
| + | 0 | - | 0 | + |
| | 極大值 |
| 極小值 |
|
由表可知:

 5分
5分
當 即
即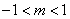 時,
時, ,
, ,
, 變化如下表
變化如下表
|
|
|
|
|
|
| - | 0 | + | 0 | - |
| | 極小值 |
| 極大值 |
|
由表可知:

 7分
7分
綜上可知:當 或
或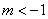 時,
時,
 ;
;
當 時,
時,
 8分
8分
(3)因為 在區間
在區間 內存在兩個極值點 ,所以
內存在兩個極值點 ,所以 ,
,
即 在
在 內有兩個不等的實根.
內有兩個不等的實根.
∴ 10分
10分
由 (1)+(3)得: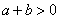 , 11分
, 11分
由(4)得: ,由(3)得:
,由(3)得: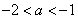 ,
,

 ,∴
,∴ .
.
故 13分
13分
考點:導數的幾何意義,應用導數研究函數的單調性、極值,二次函數的圖象和性質,不等式組的解法.


 中考解讀考點精練系列答案
中考解讀考點精練系列答案科目:高中數學 來源: 題型:
| p | x |
查看答案和解析>>
科目:高中數學 來源:2011-2012學年福建省福州市八縣(市)一中高三(上)期中數學試卷(文科)(解析版) 題型:解答題
 -2lnx、
-2lnx、查看答案和解析>>
科目:高中數學 來源:2010-2011學年福建省龍巖市高三(上)期末質量檢查一級達標數學試卷(文科)(解析版) 題型:解答題
 -2lnx、
-2lnx、查看答案和解析>>
科目:高中數學 來源:2011年福建省莆田十中高三適應性考試數學試卷(文科)(解析版) 題型:解答題
 -2lnx、
-2lnx、查看答案和解析>>
科目:高中數學 來源:2011年福建省寧德市古田縣高三適應性測試數學試卷(文科)(解析版) 題型:解答題
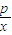 -2lnx、
-2lnx、查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com