
(06年湖南卷理)(14分)
已知橢圓![]() , 拋物線
, 拋物線![]() , 且
, 且![]() 的公共弦
的公共弦
![]() 過橢圓
過橢圓![]() 的右焦點 .
的右焦點 .
(Ⅰ) 當![]() , 求
, 求![]() 的值, 并判斷拋物線
的值, 并判斷拋物線![]() 的焦點是否在直線
的焦點是否在直線![]() 上;
上;
(Ⅱ) 是否存在![]() 的值, 使拋物線
的值, 使拋物線![]() 的焦點恰在直線
的焦點恰在直線![]() 上? 若存在, 求出符合條件的
上? 若存在, 求出符合條件的![]() 的值; 若不存在, 請說明理由 .
的值; 若不存在, 請說明理由 .
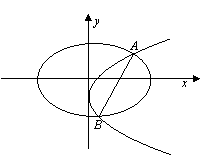
解析:(Ⅰ)當AB⊥x軸時,點A、B關于x軸對稱,所以m=0,直線AB的方程為:
x =1,從而點A的坐標為(1,![]() )或(1,-
)或(1,-![]() ). 因為點A在拋物線上.
). 因為點A在拋物線上.
所以![]() ,即
,即![]() .此時C2的焦點坐標為(
.此時C2的焦點坐標為(![]() ,0),該焦點不在直線AB上.
,0),該焦點不在直線AB上.
(II)解法一: 假設存在![]() 、
、![]() 的值使
的值使![]() 的焦點恰在直線AB上,由(I)知直線AB
的焦點恰在直線AB上,由(I)知直線AB
的斜率存在,故可設直線AB的方程為![]() .
.
由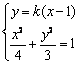 消去
消去![]() 得
得![]() ………………①
………………①
設A、B的坐標分別為(x1,y1), (x2,y2),
則x1,x2是方程①的兩根,x1+x2=![]() .
.
由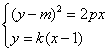
消去y得![]() . ………………②
. ………………②
因為C2的焦點![]() 在直線
在直線![]() 上,
上,
所以![]() ,即
,即![]() .代入②有
.代入②有![]() .
.
即![]() . …………………③
. …………………③
由于x1,x2也是方程③的兩根,所以x1+x2=![]() .
.
從而![]() =
=![]() . 解得
. 解得![]() ……………………④
……………………④
又AB過C1、、\、、C2的焦點,所以
![]() ,
,
則![]() …………………………………⑤
…………………………………⑤
由④、⑤式得![]() ,即
,即![]() .
.
解得![]() 于是
于是![]()
因為C2的焦點![]() 在直線
在直線![]() 上,所以
上,所以![]() .
.
![]()
![]() 或
或![]() .
.
由上知,滿足條件的![]() 、
、![]() 存在,且
存在,且![]() 或
或![]() ,
,![]() .
.
解法二:設A、B的坐標分別為![]() ,
,![]() .
.
因為AB既過C1的右焦點![]() ,又過C2的焦點
,又過C2的焦點![]() ,
,
所以![]() .
.
即![]() . ……①
. ……①
由(Ⅰ)知![]() ,于是直線AB的斜率
,于是直線AB的斜率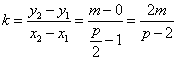 , ……②
, ……②
且直線AB的方程是![]() ,
,
所以![]() . ……③
. ……③
又因為![]() ,所以
,所以![]() . ……④
. ……④
將①、②、③代入④得![]() . ……………⑤
. ……………⑤
因為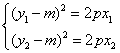 ,所以
,所以![]() . …………⑥
. …………⑥
將②、③代入⑥得![]() ……………⑦
……………⑦
由⑤、⑦得![]()
![]() 即
即![]()
解得![]() .將
.將![]() 代入⑤得
代入⑤得![]()
![]()
![]() 或
或![]() .
.
由上知,滿足條件的![]() 、
、![]() 存在,且
存在,且![]() 或
或![]() ,
,![]()


 長江作業本同步練習冊系列答案
長江作業本同步練習冊系列答案 小天才課時作業系列答案
小天才課時作業系列答案科目:高中數學 來源: 題型:
(06年湖南卷理)某外商計劃在4個候選城市投資3個不同的項目, 且在同一個城市投資的項目不超過2個, 則該外商不同的投資方案有
A. 16種 B.36種 C.42種 D.60種
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com