
【題目】已知![]() 的展開式中各項系數的和為2,則下列結論正確的有( )
的展開式中各項系數的和為2,則下列結論正確的有( )
A.![]()
B.展開式中常數項為160
C.展開式系數的絕對值的和1458
D.若![]() 為偶數,則展開式中
為偶數,則展開式中![]() 和
和![]() 的系數相等
的系數相等
【答案】ACD
【解析】
![]() 中,給
中,給![]() 賦值1求出各項系數和,列出方程求出
賦值1求出各項系數和,列出方程求出![]() ,利用二項展開式的通項公式求出通項,進而可得結果.
,利用二項展開式的通項公式求出通項,進而可得結果.
對于A,![]()
![]()
令二項式中的![]() 為1得到展開式的各項系數和為
為1得到展開式的各項系數和為![]() ,
,
![]()
![]() ,故A正確;
,故A正確;
對于B,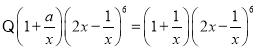
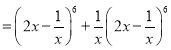 ,
,
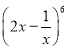 展開式的通項為
展開式的通項為![]() ,
,
當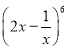 展開式是中常數項為:令
展開式是中常數項為:令![]() ,得
,得![]()
可得展開式中常數項為:![]() ,
,
當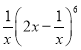 展開式是中常數項為:
展開式是中常數項為: ![]()
令![]() ,得
,得![]() (舍去)
(舍去)
故![]() 的展開式中常數項為
的展開式中常數項為![]() .故B錯誤;
.故B錯誤;
![]()
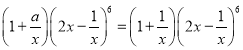
對于C,求其展開式系數的絕對值的和與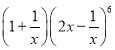 展開式系數的絕對值的和相等
展開式系數的絕對值的和相等
![]()
 ,令
,令![]() ,可得:
,可得:
![]()
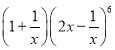 展開式系數的絕對值的和為:
展開式系數的絕對值的和為:![]() .故C正確;
.故C正確;
對于D,![]()
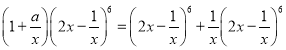
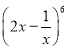 展開式的通項為
展開式的通項為![]() ,
,
當![]() 為偶數,保證展開式中
為偶數,保證展開式中![]() 和
和![]() 的系數相等
的系數相等
①![]() 和
和![]() 的系數相等,
的系數相等,
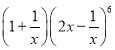 展開式系數中
展開式系數中![]() 系數為:
系數為:![]()
展開式系數中![]() 系數為:
系數為:![]()
此時![]() 和
和![]() 的系數相等,
的系數相等,
②![]() 和
和![]() 的系數相等,
的系數相等,
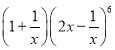 展開式系數中
展開式系數中![]() 系數為:
系數為:![]()
展開式系數中![]() 系數為:
系數為:![]()
此時![]() 和
和![]() 的系數相等,
的系數相等,
③![]() 和
和![]() 的系數相等,
的系數相等,
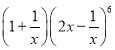 展開式系數中
展開式系數中![]() 系數為:
系數為:![]()
展開式系數中![]() 系數為:
系數為:![]()
此時![]() 和
和![]() 的系數相等,
的系數相等,
故D正確;
綜上所在,正確的是:ACD
故選:ACD.


科目:高中數學 來源: 題型:
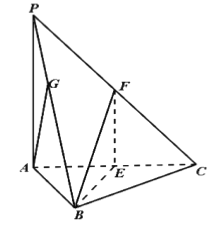
【題目】如圖,在三棱錐![]() 中,底面是邊長為4的正三角形,
中,底面是邊長為4的正三角形,![]() 底面
底面![]() ,點
,點![]() 分別為
分別為![]() 的中點,且異面直線
的中點,且異面直線![]() 和
和![]() 所成的角的大小為
所成的角的大小為![]() .
.
(1)求證:平面![]() 平面
平面![]() ;
;
(2)求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為調查某地區老年人是否需要志愿者提供幫助,用簡單隨機抽樣的方法從該地區調查了500位老年人,結果如下:
性別 是否需要志愿者 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
附:![]() 的觀測值
的觀測值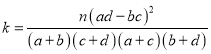
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(1)估計該地區老年人中,需要志愿者提供幫助的老年人的比例;
(2)在犯錯誤的概率不超過0.01的前提下是否可認為該地區的老年人是否需要志愿者提供幫助與性別有關?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知奇函數f(x)![]() ,函數g(θ)=cos2θ+2sinθ
,函數g(θ)=cos2θ+2sinθ![]() ,θ∈[m,
,θ∈[m,![]() ].m,b∈R.
].m,b∈R.
(1)求b的值;
(2)判斷函數f(x)在[0,1]上的單調性,并證明;
(3)當x∈[0,1]時,函數g(θ)的最小值恰為f(x)的最大值,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】用0、1、2、3、4這五個數字組成無重復數字的五位數,其中恰有一個偶數數字夾在兩個奇數數字之間的五位數的個數是( )
A.48 B.36 C.28 D.12
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高速公路服務區臨時停車場按時段收費,收費標準:每輛汽車一次停車不超過1小時收費5元,超過1小時的部分每小時收費7元(不足1小時的部分按1小時計算).現有甲、乙兩人在該服務區臨時停車,兩人停車都不超過4小時.
(1)若甲停車1小時以上且不超過2小時的概率為![]() ,停車付費多于12元的概率為
,停車付費多于12元的概率為![]() ,求甲停車付費恰為5元的概率;
,求甲停車付費恰為5元的概率;
(2)若每人停車的時長在每個時段的可能性相同,求甲、乙兩人停車付費之和為38元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個盒子中裝有1個黑球和2個白球,這3個球除顏色外完全相同.有放回地連續抽取2次,每次從中任意地取出1個球.計算下列事件的概率:
(1)取出的兩個球都是白球;
(2)第一次取出白球,第二取出黑球;
(3)取出的兩個球中至少有一個白球.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出如圖所示的三幅統計圖及四個命題:
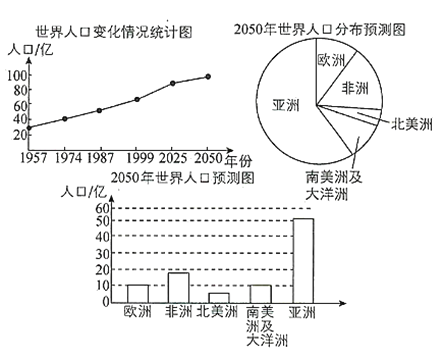
①從折線圖能看出世界人口的變化情況;
②2050年非洲人口將達到大約15億;
③2050年亞洲人口比其他各洲人口的總和還要多;
④從1957年到2050年各洲中北美洲人口增長速度最慢.
其中命題正確的有( )
A.①②B.①③C.①④D.②④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com