【題目】已知函數
.
（1）當
時，求
的單調區間；
（2）若函數在
上無零點，求
最小值.
【答案】(1) 
的單調減區為
，單調增區間為
,(2) 
的最小值為
．
【解析】試題解析: （I）代入a的值，寫出函數的解析式，對函數求導，使得導函數大于0，求出自變量的值，寫出單調區間．
（II）根據函數無零點，得到函數的導函數小于0在一個區間上不恒成立，得到函數在這個區間上沒有零點，構造新函數，對函數求導，利用求最值得方法求出函數的最小值．
（1）當
時，
，
則
，由
，得
，由
，得
，
故的單調減區為，單調增區間為.
（2）因為在區間
上恒成立不可能，
故要使函數在上無零點，只要對任意的
，恒成立，即對
恒成立，令
，則
，再令
，則
，故
在上為減函數，于是
，從而
，于是
在上為增函數，所以
，故要使
恒成立，只要
，綜上，若函數在上無零點，則的最小值為
.
活力課時同步練習冊系列答案科目：高中數學 來源： 題型：
【題目】已知函數f（x）=lg（x+1），g（x）=2lg（2x+t）（t為參數）．
（1）寫出函數f（x）的定義域和值域；
（2）當x∈[0，1]時，如果f（x）≤g（x），求參數t的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（12分）如圖，橢圓
（
）的離心率
，短軸的兩個端點分別為B1、B2，焦點為F1、F2，四邊形F1 B1F2 B2的內切圓半徑為
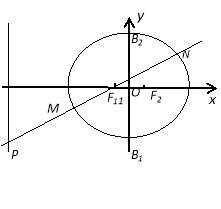
（1）求橢圓C的方程；
（2）過左焦點F1的直線交橢圓于M、N兩點，交直線
于點P，設
，
，試證
為定值，并求出此定值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設全集為實數集R，函數f（x）=lg（2x﹣1）的定義域為A，集合B={x||x|﹣a≤0}（a∈R）
（1）若a=2，求A∪B和A∩B
（2）若RA∪B=RA，求a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知定理：“實數m，n為常數，若函數h（x）滿足h（m+x）+h（m﹣x）=2n，則函數y=h（x）的圖象關于點（m，n）成中心對稱”．
（1）已知函數f（x）= 
的圖象關于點（1，b）成中心對稱，求實數b的值；
（2）已知函數g（x）滿足g（2+x）+g（﹣x）=4，當x∈[0，2]時，都有g（x）≤3成立，且當x∈[0，1]時，g（x）=2k（x﹣1）+1 ， 求實數k的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在三棱錐P－ABC中，PA⊥AB，PA⊥BC，AB⊥BC，PA＝AB＝BC＝2，D為線段AC的中點，E為線段PC上一點.
(1)求證：PA⊥BD；
(2)求證：平面BDE⊥平面PAC；
(3)當PA∥平面BDE時，求三棱錐E－BCD的體積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在△OAB中，點P為線段AB上的一個動點（不包含端點），且滿足 
=λ 
． 
（1）若λ= 
，用向量 
， 
表示 
；
（2）若| |=4，| |=3，且∠AOB=60°，求 
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了解某單位員工的月工資水平，從該單位500位員工中隨機抽取了50位進行調查，得到如下頻數分布表和頻率分布直方圖：
月工資 | [15，25） | [25，35） | [35，45） | [45，55） | [55，65） | [65，75） |
男員工數 | 1 | 8 | 10 | 6 | 4 | 4 |
女員工數 | 4 | 2 | 5 | 4 | 1 | 1 |
（1）試由圖估計該單位員工月平均工資；
（2）現用分層抽樣的方法從月工資在[45，55）和[55，65）的兩組所調查的男員工中隨機選取5人，問各應抽取多少人？
（3）若從月工資在[25，35）和[45，55）兩組所調查的女員工中隨機選取2人，試求這2人月工資差不超過1000元的概率．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
