Question

如圖15，把等腰Rt△ABC沿斜邊AB旋轉至△ABD的位置，使CD＝AC,

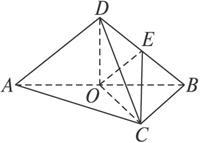
圖15

（1）求證：平面ABD⊥平面ABC；

（2）求二面角C-BD-A的余弦值.

Answer 1

（1）證法一:由題設,知AD＝CD＝BD,作DO⊥平面ABC，O為垂足，則OA＝OB＝OC.

∴O是△ABC的外心，即AB的中點.

∴O∈AB，即O∈平面ABD.

∴OD平面ABD.∴平面ABD⊥平面ABC.

證法二:取AB中點O，連接OD、OC,

則有OD⊥AB，OC⊥AB，即∠COD是二面角CABD的平面角.

設AC＝a，則OC＝OD＝a,

又CD＝AD＝AC,∴CD＝a.∴△COD是直角三角形，即∠COD＝90°.

∴二面角是直二面角，即平面ABD⊥平面ABC.

（2）解:取BD的中點E，連接CE、OE、OC,∵△BCD為正三角形，∴CE⊥BD.

又△BOD為等腰直角三角形,∴OE⊥BD.∴∠OEC為二面角C-BD-A的平面角.

同（1）可證OC⊥平面ABD,∴OC⊥OE.∴△COE為直角三角形.

設BC＝a，則CE＝a，OE＝a,∴cos∠OEC＝＝即為所求.