(本小題滿分12分)如圖,在三棱柱
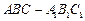
中,已知
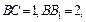
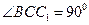
,
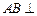
側(cè)面
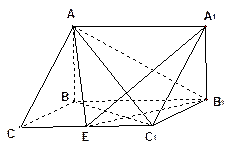
(1)求直線C
1B與底面ABC所成角的正弦值;
(2)在棱
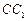
(不包含端點
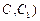
上確定一點
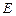
的位置,使得
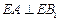
(要求說明理由).
(3)在(2)的條件下,若
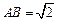
,求二面角
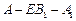
的大小.
(1)
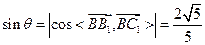
(2)
(3) 45°.
解::如圖,以
B為原點建立空間直角坐標系,則
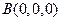
,
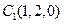
,
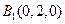
……1分
(1)直三棱柱
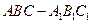
中,
平面
的法向量
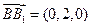
,又
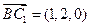
,
設(shè)
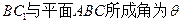
,則
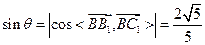
…………4分
(2)設(shè)
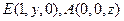

,則
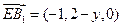
,
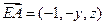
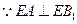
,∴
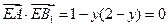
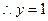
,即
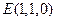
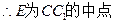
…………8

分
(3)∵
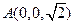
,則
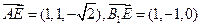
,設(shè)平面
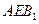
的法向量

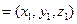
,則
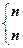
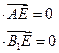
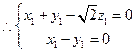
,取
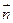
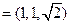
,…………10分
∵
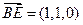
,

∴
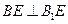
,又
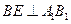
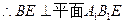
,
∴平面

的法向量
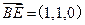
,∴
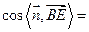
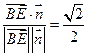
,
∴二面角
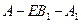
為45°. …………12分
練習冊系列答案
相關(guān)習題
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分12分)如圖所示,在正方體
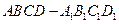
中,
E為AB的中點
(1)若
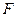
為
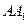
的中點,求證:
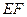
∥面
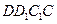
;
(2) 若
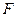
為
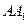
的中點,求二面角
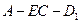
的余弦值;
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
正四棱錐所有棱長均為2,則側(cè)棱和底面所成的角是 ( )
| A. 30° | B. 45° | C. 60 ° | D. 90° |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分13分)
如圖,已知四棱錐
P-
ABCD的底面是菱形,∠
BCD=60°,點
E是
BC邊的中點,
AC與
DE交于點
O,
PO⊥平面
ABCD.
(Ⅰ)求證:
PD⊥
BC;
(Ⅱ)若
AB=6,
PC=6,求二面角
P-
AD-
C的大小;
(Ⅲ)在(Ⅱ)的條件下,求異面直線
PB與
DE所成角的余弦值.

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(12分)設(shè)圓臺的高為3,其軸截面(過圓臺軸的截面)如圖
所示,母線
A1A與

底面圓的直徑
AB的夾角為
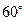
,在軸截面中
A1B⊥
A1A,求圓臺的體積
V.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
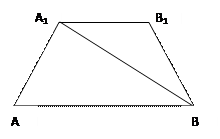
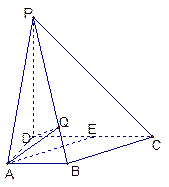
(本小題滿分12分)
四棱錐
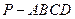
中,側(cè)棱
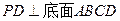
,底面
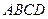
是直角梯形,
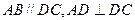
,且
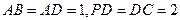
,
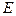
是
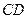
的中點

.
(I)求異面直線
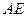
與
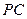
所成的角;
(II)線段
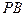

上是否存在一點
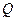
,使得
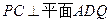
?若存在,求出
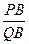
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
如圖,在四面體ABCD中,若截面PQMN是正方形,則在下列命題中,錯誤的是( )
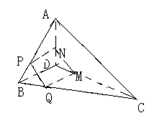
A AC⊥BD B AC∥截面PQMN C AC=BD D PM與BD所成角為450
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
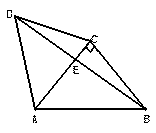
(本小題共12分) 如圖,△ACD是等邊三角形,△ABC是等腰直角
三角形,∠ACB=90°,BD交AC于E,AB=2.
(1)求cos∠CBE的值;(2)求AE。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知直線
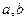
和平面
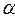
,且
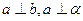
,則
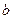
與
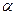
的位置關(guān)系是______________
查看答案和解析>>

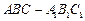 中,已知
中,已知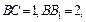
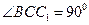 ,
,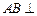 側(cè)面
側(cè)面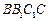

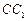 (不包含端點
(不包含端點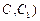 上確定一點
上確定一點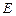 的位置,使得
的位置,使得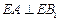 (要求說明理由).
(要求說明理由).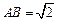 ,求二面角
,求二面角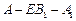 的大小.
的大小.
 底面圓的直徑AB的夾角為
底面圓的直徑AB的夾角為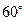 ,在軸截面中
,在軸截面中
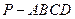 中,側(cè)棱
中,側(cè)棱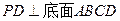 ,底面
,底面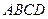 是直角梯形,
是直角梯形,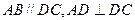 ,且
,且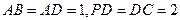 ,
,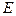 是
是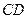 的中點
的中點 .
.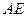 與
與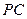 所成的角;
所成的角;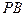
 上是否存在一點
上是否存在一點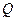 ,使得
,使得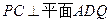 ?若存在,求出
?若存在,求出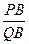 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.

