
【題目】已知函數![]() .
.
(1)當![]() 時,求
時,求![]() 的單調區間;
的單調區間;
(2)若![]() 在
在![]() 處取得極大值,求
處取得極大值,求![]() 的取值范圍.
的取值范圍.
科目:高中數學 來源: 題型:
【題目】2021年我省將實施新高考,新高考“依據統一高考成績、高中學業水平考試成績,參考高中學生綜合素質評價信息”進行人才選拔。我校2018級高一年級一個學習興趣小組進行社會實踐活動,決定對某商場銷售的商品A進行市場銷售量調研,通過對該商品一個階段的調研得知,發現該商品每日的銷售量![]() (單位:百件)與銷售價格
(單位:百件)與銷售價格![]() (元/件)近似滿足關系式
(元/件)近似滿足關系式![]() ,其中
,其中![]() 為常數
為常數![]() 已知銷售價格為3元/件時,每日可售出該商品10百件。
已知銷售價格為3元/件時,每日可售出該商品10百件。
(1)求函數![]() 的解析式;
的解析式;
(2)若該商品A的成本為2元/件,根據調研結果請你試確定該商品銷售價格的值,使該商場每日銷售該商品所獲得的利潤(單位:百元)最大。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市環保部門為了讓全市居民認識到冬天燒煤取暖對空氣![]() 數值的影響,進而喚醒全市人民的環保節能意識。對該市取暖季燒煤天數
數值的影響,進而喚醒全市人民的環保節能意識。對該市取暖季燒煤天數![]() 與空氣
與空氣![]() 數值不合格的天數
數值不合格的天數![]() 進行統計分析,得出下表數據:
進行統計分析,得出下表數據:
| 9 | 8 | 7 | 5 | 4 |
| 7 | 6 | 5 | 3 | 2 |
(1)以統計數據為依據,求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)根據(1)求出的線性回歸方程,預測該市燒煤取暖的天數為20時空氣![]() 數值不合格的天數.
數值不合格的天數.
參考公式: ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知點![]() ,點
,點![]() 均在圓
均在圓![]() 上,且
上,且![]() ,過點
,過點![]() 作
作![]() 的平行線分別交
的平行線分別交![]() ,
,![]() 于
于![]() 兩點.
兩點.
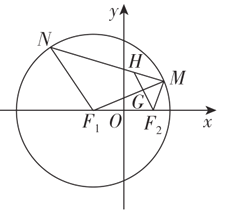
(1)求點![]() 的軌跡方程;
的軌跡方程;
(2)過點![]() 的動直線
的動直線![]() 與點
與點![]() 的軌跡交于
的軌跡交于![]() 兩點.問是否存在常數
兩點.問是否存在常數![]() ,使得
,使得![]() 點為定值?若存在,求出
點為定值?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲袋中裝有2個白球,3個黑球,乙袋中裝有1個白球,2個黑球,這些球除顏色外完全相同.
(1)從兩袋中各取1個球,記事件![]() :取出的2個球均為白球,求
:取出的2個球均為白球,求![]() ;
;
(2)每次從甲、乙兩袋中各取2個球,若取出的白球不少于2個就獲獎(每次取完后將球放回原袋),共取了3次,記獲獎次數為![]() ,寫出
,寫出![]() 的分布列并求
的分布列并求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知命題![]() :函數
:函數![]() 在定義域
在定義域![]() 上單調遞增;命題
上單調遞增;命題![]() :
:![]() 在區間
在區間![]() 上恒成立.
上恒成立.
(1)如果命題![]() 為真命題,求實數
為真命題,求實數![]() 的值或取值范圍;
的值或取值范圍;
(2)命題“![]() ”為真命題,“
”為真命題,“![]() ”為假命題,求實數
”為假命題,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com